Control of a Cart-Pole Dynamic System with TF-Agents

1. Introduction

The cart-pole problem can be considered as the “Hello World” problem of Reinforcement Learning (RL). It was described by Barto (1983). The physics of the system is as follows:

• All motion happens in a vertical plane
• A hinged pole is attached to a cart
• The cart slides horizontally on a track in an effort to balance the pole vertically
• The system has four state variables:

\(x\): displacement of the cart

\(\theta\): vertical angle on the pole

\(\dot{x}\): velocity of the cart

\(\dot{\theta}\): angular velocity of the pole

Here is a graphical representation of the system:

Cartpole environment

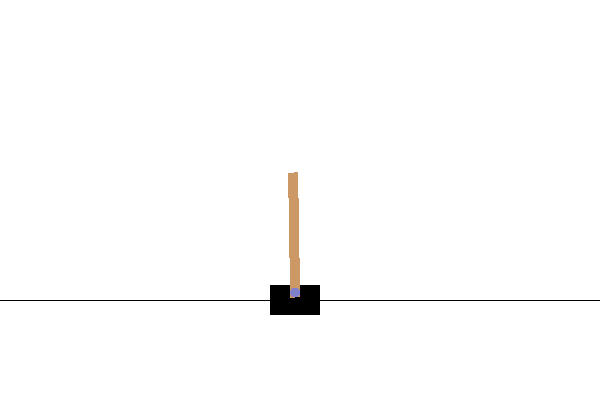
2. Purpose

The purpose of our activity in this blog post is to construct and train an entity, let’s call it a controller, that can manage the horizontal motions of the cart so that the pole remains as close to vertical as possible. The controlled entity is, of course, the cart and pole system.

3. TF-Agents Setup

We will use the Tensorflow TF-Agents framework. In addition, this notebook will need to run in Google Colab.

from __future__ import absolute_import, division, print_function
import base64
import imageio
import IPython
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import PIL.Image
import pyvirtualdisplay
import tensorflow as tf
from tf_agents.agents.dqn import dqn_agent
from tf_agents.drivers import dynamic_step_driver
from tf_agents.environments import suite_gym
from tf_agents.environments import tf_py_environment
from tf_agents.eval import metric_utils
from tf_agents.metrics import tf_metrics
from tf_agents.networks import q_network
from tf_agents.policies import random_tf_policy
from tf_agents.replay_buffers import tf_uniform_replay_buffer
from tf_agents.trajectories import trajectory
from tf_agents.utils import common

tf.version.VERSION

'2.4.0'

The following is needed for rendering a virtual display:

tf.compat.v1.enable_v2_behavior()
display = pyvirtualdisplay.Display(visible=0, size=(1400, 900)).start()

4. Hyperparameters

Here we specify all the hyperparameters for the problem:

NUM_ITERATIONS = 20000

INITIAL_COLLECT_STEPS = 100
COLLECT_STEPS_PER_ITERATION = 1
REPLAY_BUFFER_MAX_LENGTH = 100000

BATCH_SIZE = 64
LEARNING_RATE = 1e-3
LOG_INTERVAL = 200

NUM_EVAL_EPISODES = 10
EVAL_INTERVAL = 1000

5. Graphical Representation of the Problem

We will work with a graphical representation of our cart-and-pole problem, rather than to just ramble on with words. This will enhance the description. The graphic will also include some TF-Agents specifics. Here is the representation:

Figure 1 Graphical Representation

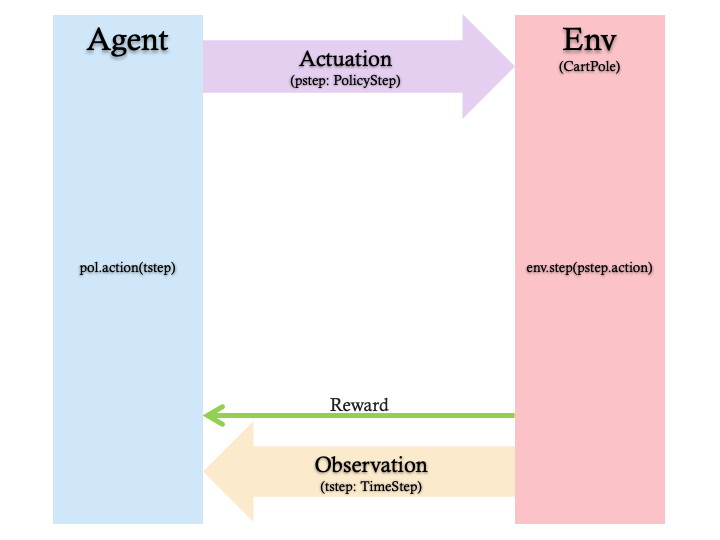
6. Environment

Let’s start with the controller. In Reinforcement Learning, the controlled entity is known as an environment. The TF-Agents framework contain some ready to use environments that can be created in TF-Agents using the tf_agents.environments suites. Fortunately, it makes access to the cart-and-pole environment (setup by OpenAI Gym) easy. Next, we load the cart-and-pole environment from the OpenAI Gym suite.

env_name = 'CartPole-v0'
env = suite_gym.load(env_name)

You can render this environment to see how it looks. A free-swinging pole is attached to a cart. The goal is to move the cart right or left in order to keep the pole pointing up. To verify, we can inspect our loaded environment with:

env.reset()
PIL.Image.fromarray(env.render())

Input to Environment

The specification of inputs to the environment is provided by the env.action_spec method:

env.action_spec()

BoundedArraySpec(shape=(), dtype=dtype('int64'), name='action', minimum=0, maximum=1)

shape specifies the structure of the input which is a scalar in this case. dtype is the data type which is an int64. The minimum value of the action is 0 and the maximum is 1. We will use the convention that the action on the cart is as follows:

• 0 means LEFT
• 1 means RIGHT

Evolution of the Environment

The arrival of an action at the input of the environment leads to the update of its state. This is how the environment evolves. To advance the state of the environment, the environment.step method takes an input action and returns a TimeStep tuple containing the next observation of the environment and the reward for the action.

Output from Environment

The specification of output from the environment is provided by the env.time_step_spec method:

env.time_step_spec()

TimeStep(step_type=ArraySpec(shape=(), dtype=dtype('int32'), name='step_type'), reward=ArraySpec(shape=(), dtype=dtype('float32'), name='reward'), discount=BoundedArraySpec(shape=(), dtype=dtype('float32'), name='discount', minimum=0.0, maximum=1.0), observation=BoundedArraySpec(shape=(4,), dtype=dtype('float32'), name='observation', minimum=[-4.8000002e+00 -3.4028235e+38 -4.1887903e-01 -3.4028235e+38], maximum=[4.8000002e+00 3.4028235e+38 4.1887903e-01 3.4028235e+38]))

This specification has the following fields:

env.time_step_spec()._fields

('step_type', 'reward', 'discount', 'observation')

The step_type indicates whether a step is the first step, a middle step, or the last step in an episode:

env.time_step_spec().step_type

ArraySpec(shape=(), dtype=dtype('int32'), name='step_type')

The reward is a scalar which conveys the reward from the environment:

env.time_step_spec().reward

ArraySpec(shape=(), dtype=dtype('float32'), name='reward')

The discount is a factor that modifies the reward:

env.time_step_spec().discount

BoundedArraySpec(shape=(), dtype=dtype('float32'), name='discount', minimum=0.0, maximum=1.0)

The observation is the observable state of the environment:

env.time_step_spec().observation

BoundedArraySpec(shape=(4,), dtype=dtype('float32'), name='observation', minimum=[-4.8000002e+00 -3.4028235e+38 -4.1887903e-01 -3.4028235e+38], maximum=[4.8000002e+00 3.4028235e+38 4.1887903e-01 3.4028235e+38])

In this case we have a vector with 4 elements - one each for the cart displacement, cart velocity, pole angle, and pole angular velocity.

Demonstrate the evolution of the environment

Let’s submit 10 RIGHT actions to the environment, just for fun:

It is interesting to see an agent actually performing a task in an environment.

First, create a function to embed videos in the notebook.

def embed_mp4(filename):
  """Embeds an mp4 file in the notebook."""
  video = open(filename,'rb').read()
  b64 = base64.b64encode(video)
  tag = '''
  <video width="640" height="480" controls>
    <source src="data:video/mp4;base64,{0}" type="video/mp4">
  Your browser does not support the video tag.
  </video>'''.format(b64.decode())

  return IPython.display.HTML(tag)

Now iterate through a few episodes of the Cartpole game with the agent. The underlying Python environment (the one “inside” the TensorFlow environment wrapper) provides a render() method, which outputs an image of the environment state. These can be collected into a video.

def create_video(filename, action, num_steps=10, fps=30):
  filename = filename + ".mp4"
  env.reset()
  with imageio.get_writer(filename, fps=fps) as video:
    video.append_data(env.render())
    for _ in range(num_steps):
      tstep = env.step(action); print(tstep)
      video.append_data(env.render())
  return embed_mp4(filename)

action = np.array(1, dtype=np.int32) #move RIGHT action

create_video("untrained-agent", action, 50)

WARNING:root:IMAGEIO FFMPEG_WRITER WARNING: input image is not divisible by macro_block_size=16, resizing from (400, 600) to (400, 608) to ensure video compatibility with most codecs and players. To prevent resizing, make your input image divisible by the macro_block_size or set the macro_block_size to None (risking incompatibility). You may also see a FFMPEG warning concerning speedloss due to data not being aligned.

TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([-0.02020498,  0.21937552, -0.02017608, -0.34391108], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([-0.01581747,  0.4147786 , -0.0270543 , -0.6428874 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([-0.0075219 ,  0.610267  , -0.03991205, -0.9439657 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.00468344,  0.80590326, -0.05879136, -1.2489173 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.0208015 ,  1.0017276 , -0.08376971, -1.5594211 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.04083605,  1.1977463 , -0.11495813, -1.8770176 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.06479098,  1.3939193 , -0.15249848, -2.2030582 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.09266937,  1.5901439 , -0.19655965, -2.5386403 ], dtype=float32))
TimeStep(step_type=array(2, dtype=int32), reward=array(1., dtype=float32), discount=array(0., dtype=float32), observation=array([ 0.12447225,  1.7862376 , -0.24733245, -2.8845341 ], dtype=float32))
TimeStep(step_type=array(0, dtype=int32), reward=array(0., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.01009047, -0.03597898,  0.02516665,  0.00526722], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.00937089,  0.15877317,  0.02527199, -0.27937028], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.01254635,  0.35352567,  0.01968459, -0.5639766 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.01961686,  0.54836595,  0.00840506, -0.85039353], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.03058418,  0.7433723 , -0.00860281, -1.1404216 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.04545163,  0.93860567, -0.03141125, -1.4357901 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.06422374,  1.1341006 , -0.06012705, -1.738121  ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.08690576,  1.3298539 , -0.09488947, -2.0488873 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.11350283,  1.5258118 , -0.13586721, -2.3693573 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.14401907,  1.7218534 , -0.18325436, -2.700532  ], dtype=float32))
TimeStep(step_type=array(2, dtype=int32), reward=array(1., dtype=float32), discount=array(0., dtype=float32), observation=array([ 0.17845613,  1.9177724 , -0.23726499, -3.0430653 ], dtype=float32))
TimeStep(step_type=array(0, dtype=int32), reward=array(0., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.043414  ,  0.03911114, -0.04063306, -0.04680319], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.04419622,  0.23479147, -0.04156913, -0.35202426], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.04889205,  0.43047914, -0.04860961, -0.65752   ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.05750163,  0.6262428 , -0.06176001, -0.9651042 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.07002649,  0.82213753, -0.0810621 , -1.276532  ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.08646924,  1.0181942 , -0.10659274, -1.5934575 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.10683312,  1.2144072 , -0.13846189, -1.9173855 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.13112126,  1.410721  , -0.1768096 , -2.2496157 ], dtype=float32))
TimeStep(step_type=array(2, dtype=int32), reward=array(1., dtype=float32), discount=array(0., dtype=float32), observation=array([ 0.15933569,  1.6070133 , -0.2218019 , -2.5911756 ], dtype=float32))
TimeStep(step_type=array(0, dtype=int32), reward=array(0., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.02383677,  0.03858507, -0.03498537, -0.00475328], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.02460848,  0.23419084, -0.03508044, -0.30826598], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.02929229,  0.4297946 , -0.04124576, -0.6118027 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.03788818,  0.625468  , -0.05348181, -0.91718596], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.05039755,  0.8212707 , -0.07182553, -1.2261863 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.06682296,  1.01724   , -0.09634926, -1.540481  ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.08716776,  1.2133797 , -0.12715888, -1.8616087 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.11143535,  1.409646  , -0.16439106, -2.1909153 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.13962828,  1.6059324 , -0.20820937, -2.5294888 ], dtype=float32))
TimeStep(step_type=array(2, dtype=int32), reward=array(1., dtype=float32), discount=array(0., dtype=float32), observation=array([ 0.17174692,  1.8020512 , -0.25879914, -2.878086  ], dtype=float32))
TimeStep(step_type=array(0, dtype=int32), reward=array(0., dtype=float32), discount=array(1., dtype=float32), observation=array([-0.04581273, -0.04085314, -0.0127504 ,  0.04206099], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([-0.0466298 ,  0.15444931, -0.01190918, -0.2546174 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([-0.04354081,  0.34973925, -0.01700153, -0.5510328 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([-0.03654603,  0.5450958 , -0.02802218, -0.84902346], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([-0.02564411,  0.7405885 , -0.04500265, -1.1503848 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([-0.01083234,  0.9362679 , -0.06801035, -1.4568331 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.00789302,  1.1321553 , -0.09714701, -1.7699646 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.03053613,  1.3282304 , -0.1325463 , -2.0912066 ], dtype=float32))
TimeStep(step_type=array(1, dtype=int32), reward=array(1., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.05710074,  1.5244164 , -0.17437044, -2.4217591 ], dtype=float32))
TimeStep(step_type=array(2, dtype=int32), reward=array(1., dtype=float32), discount=array(0., dtype=float32), observation=array([ 0.08758906,  1.7205641 , -0.22280562, -2.7625246 ], dtype=float32))
TimeStep(step_type=array(0, dtype=int32), reward=array(0., dtype=float32), discount=array(1., dtype=float32), observation=array([ 0.00606389, -0.01771289, -0.02044516, -0.03224904], dtype=float32))

We are not surprised to see the pole repeatedly falling over to the left as the agent repeatedly applies an action to the right.

We will use two environments: one for training and one for evaluation.

train_py_env = suite_gym.load(env_name)
eval_py_env = suite_gym.load(env_name)

Convert environments to TensorFlow

The Cartpole environment, like most environments, is written in pure Python. This is converted to TensorFlow using the TFPyEnvironment wrapper.

The original environment’s API uses Numpy arrays. The TFPyEnvironment converts these to Tensors to make it compatible with Tensorflow agents and policies.

train_env = tf_py_environment.TFPyEnvironment(train_py_env)
eval_env = tf_py_environment.TFPyEnvironment(eval_py_env)

7. Agent

The controller in our problem is the algorithm used to solve the problem. In RL parlance the controller is known as an Agent. TF-Agents provides standard implementations of a variety of Agents, including:

• DQN
• REINFORCE
• DDPG
• TD3
• PPO
• SAC.

For our problem we will use the DQN agent. The DQN agent can be used in any environment which has a discrete action space.

The fundamental problem for an Agent is how to find the next best action to submit to the environment. In the case of a DQN Agent the agent makes use of a QNetwork, which is a neural network model that can learn to predict QValues (expected returns) for all actions, given an observation from the environment. By inspecting the QValues, the agent can decide on the best next action.

QNetwork

We use tf_agents.networks.q_network to create a QNetwork, passing in the observation_spec, action_spec, and a tuple fc_layer_params describing the number and size of the model’s hidden layers. Each value in the tuple specifies the number of neurons for that hidden layer:

fc_layer_params = (100,)
q_net = q_network.QNetwork(
    input_tensor_spec= train_env.observation_spec(), 
    action_spec=       train_env.action_spec(), 
    fc_layer_params=   fc_layer_params)

DqnAgent

We now use tf_agents.agents.dqn.dqn_agent to instantiate a DqnAgent. In addition to the time_step_spec, action_spec and the QNetwork, the agent constructor also requires an optimizer (in this case, AdamOptimizer), a loss function, and an integer step counter.

optimizer = tf.compat.v1.train.AdamOptimizer(learning_rate=LEARNING_RATE)
train_step_counter = tf.Variable(0)
agent = dqn_agent.DqnAgent(
    time_step_spec=     train_env.time_step_spec(),
    action_spec=        train_env.action_spec(),
    q_network=          q_net,
    optimizer=          optimizer,
    td_errors_loss_fn=  common.element_wise_squared_loss,
    train_step_counter= train_step_counter)
agent.initialize()

Policies

A policy defines the way an agent acts relative to the environment. The goal of reinforcement learning is to train the underlying model until the policy produces the desired outcome.

In this problem:

• The desired outcome is keeping the pole balanced vertically over the cart
• The policy returns an action (LEFT or RIGHT) for each TimeStep’s observation

Agents contain two policies:

• agent.policy — The main policy that is used for evaluation and deployment.
• agent.collect_policy — A second policy that is used for data collection.

eval_policy = agent.policy
eval_policy

<tf_agents.policies.greedy_policy.GreedyPolicy at 0x7f1bda2d40f0>

collect_policy = agent.collect_policy
collect_policy

<tf_agents.policies.epsilon_greedy_policy.EpsilonGreedyPolicy at 0x7f1bda2cce10>

Policies can be created independently of agents. For example, use tf_agents.policies.random_tf_policy to create a policy which will randomly select an action for each time_step.

random_policy = random_tf_policy.RandomTFPolicy(
    time_step_spec= train_env.time_step_spec(), 
    action_spec=    train_env.action_spec())

To get an action from a policy, call the policy.action(tstep) method. The tstep of type TimeStep contains the observation from the environment. This method returns a PolicyStep, which is a named tuple with three components:

• action — the action to be taken (in this case, 0 or 1)
• state — used for stateful (that is, RNN-based) policies
• info — auxiliary data, such as log probabilities of actions

Let’s create an example environment and setup a random policy:

example_environment = tf_py_environment.TFPyEnvironment(
    suite_gym.load('CartPole-v0'))

We reset this environment:

tstep = example_environment.reset()
tstep

TimeStep(step_type=<tf.Tensor: shape=(1,), dtype=int32, numpy=array([0], dtype=int32)>, reward=<tf.Tensor: shape=(1,), dtype=float32, numpy=array([0.], dtype=float32)>, discount=<tf.Tensor: shape=(1,), dtype=float32, numpy=array([1.], dtype=float32)>, observation=<tf.Tensor: shape=(1, 4), dtype=float32, numpy=
array([[-0.01827296,  0.03853731,  0.0239976 , -0.03041968]],
      dtype=float32)>)

tstep._fields

('step_type', 'reward', 'discount', 'observation')

print(tstep.step_type)
print(tstep.reward)
print(tstep.discount)
print(tstep.observation)

tf.Tensor([0], shape=(1,), dtype=int32)
tf.Tensor([0.], shape=(1,), dtype=float32)
tf.Tensor([1.], shape=(1,), dtype=float32)
tf.Tensor([[-0.01827296  0.03853731  0.0239976  -0.03041968]], shape=(1, 4), dtype=float32)

Now we find the PolicyStep from which the next action can be found:

pstep = random_policy.action(tstep)
pstep

PolicyStep(action=<tf.Tensor: shape=(1,), dtype=int64, numpy=array([0])>, state=(), info=())

pstep._fields

('action', 'state', 'info')

print(pstep.action)
print(pstep.state)
print(pstep.info)

tf.Tensor([0], shape=(1,), dtype=int64)
()
()

8. Metrics and Evaluation

The most common metric used to evaluate a policy is the average return. The return is the sum of rewards obtained while running a policy in an environment for an episode. Several episodes are run, creating an average return.

The following function computes the average return of a policy, given the policy, environment, and a number of episodes.

def compute_avg_return(env, pol, num_episodes=10):
  total_return = 0.0
  for _ in range(num_episodes):
    tstep = env.reset()
    episode_return = 0.0
    while not tstep.is_last():
      pstep = pol.action(tstep)
      tstep = env.step(pstep.action)
      episode_return += tstep.reward
    total_return += episode_return
  avg_return = total_return / num_episodes
  return avg_return.numpy()[0]
# See also the metrics module for standard implementations of different metrics.
# https://github.com/tensorflow/agents/tree/master/tf_agents/metrics

Running this computation on the random_policy shows a baseline performance in the environment.

NUM_EVAL_EPISODES

10

compute_avg_return(eval_env, random_policy, NUM_EVAL_EPISODES)

19.2

9. Replay Buffer

The replay buffer keeps track of data collected from the environment. We will use tf_agents.replay_buffers.tf_uniform_replay_buffer.TFUniformReplayBuffer, as it is the most common.

The constructor requires the specs for the data it will be collecting. This is available from the agent using the collect_data_spec method. The batch size and maximum buffer length are also required.

replay_buffer = tf_uniform_replay_buffer.TFUniformReplayBuffer(
    data_spec=  agent.collect_data_spec,
    batch_size= train_env.batch_size,
    max_length= REPLAY_BUFFER_MAX_LENGTH)

For most agents, collect_data_spec is a named tuple called Trajectory, containing the specs for observations, actions, rewards, and other items.

agent.collect_data_spec

Trajectory(step_type=TensorSpec(shape=(), dtype=tf.int32, name='step_type'), observation=BoundedTensorSpec(shape=(4,), dtype=tf.float32, name='observation', minimum=array([-4.8000002e+00, -3.4028235e+38, -4.1887903e-01, -3.4028235e+38],
      dtype=float32), maximum=array([4.8000002e+00, 3.4028235e+38, 4.1887903e-01, 3.4028235e+38],
      dtype=float32)), action=BoundedTensorSpec(shape=(), dtype=tf.int64, name='action', minimum=array(0), maximum=array(1)), policy_info=(), next_step_type=TensorSpec(shape=(), dtype=tf.int32, name='step_type'), reward=TensorSpec(shape=(), dtype=tf.float32, name='reward'), discount=BoundedTensorSpec(shape=(), dtype=tf.float32, name='discount', minimum=array(0., dtype=float32), maximum=array(1., dtype=float32)))

agent.collect_data_spec._fields

('step_type',
 'observation',
 'action',
 'policy_info',
 'next_step_type',
 'reward',
 'discount')

10. Data Collection

Now we execute the random policy in the environment for a few steps, recording the data in the replay buffer.

def collect_step(env, pol, buffer):
  tstep = env.current_time_step()
  pstep = pol.action(tstep)
  next_tstep = env.step(pstep.action)
  traj = trajectory.from_transition(tstep, pstep, next_tstep)
  buffer.add_batch(traj) # Add trajectory to the replay buffer

def collect_data(env, pol, buffer, steps):
  for _ in range(steps):
    collect_step(env, pol, buffer)

collect_data(train_env, random_policy, replay_buffer, INITIAL_COLLECT_STEPS)

# This loop is so common in RL, that we provide standard implementations. 
# For more details see the drivers module.
# https://www.tensorflow.org/agents/api_docs/python/tf_agents/drivers

The replay buffer is now a collection of Trajectories. Let’s inspect one of the Trajectories:

traj = iter(replay_buffer.as_dataset()).next()
print(type(traj))
print(len(traj))
print(traj);

<class 'tuple'>
2
(Trajectory(step_type=<tf.Tensor: shape=(), dtype=int32, numpy=2>, observation=<tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.00616293, -0.2612567 ,  0.23251233,  1.5463613 ], dtype=float32)>, action=<tf.Tensor: shape=(), dtype=int64, numpy=1>, policy_info=(), next_step_type=<tf.Tensor: shape=(), dtype=int32, numpy=0>, reward=<tf.Tensor: shape=(), dtype=float32, numpy=0.0>, discount=<tf.Tensor: shape=(), dtype=float32, numpy=1.0>), BufferInfo(ids=<tf.Tensor: shape=(), dtype=int64, numpy=29>, probabilities=<tf.Tensor: shape=(), dtype=float32, numpy=0.01>))

traj[0]

Trajectory(step_type=<tf.Tensor: shape=(), dtype=int32, numpy=2>, observation=<tf.Tensor: shape=(4,), dtype=float32, numpy=array([-0.00616293, -0.2612567 ,  0.23251233,  1.5463613 ], dtype=float32)>, action=<tf.Tensor: shape=(), dtype=int64, numpy=1>, policy_info=(), next_step_type=<tf.Tensor: shape=(), dtype=int32, numpy=0>, reward=<tf.Tensor: shape=(), dtype=float32, numpy=0.0>, discount=<tf.Tensor: shape=(), dtype=float32, numpy=1.0>)

type(traj[0])

tf_agents.trajectories.trajectory.Trajectory

traj[0]._fields

('step_type',
 'observation',
 'action',
 'policy_info',
 'next_step_type',
 'reward',
 'discount')

print('step_type:', traj[0].step_type)
print('observation:', traj[0].observation)
print('action:', traj[0].action)
print('policy_info:', traj[0].policy_info)
print('next_step_type:', traj[0].next_step_type)
print('reward:', traj[0].reward)
print('discount:', traj[0].discount)

step_type: tf.Tensor(2, shape=(), dtype=int32)
observation: tf.Tensor([-0.00616293 -0.2612567   0.23251233  1.5463613 ], shape=(4,), dtype=float32)
action: tf.Tensor(1, shape=(), dtype=int64)
policy_info: ()
next_step_type: tf.Tensor(0, shape=(), dtype=int32)
reward: tf.Tensor(0.0, shape=(), dtype=float32)
discount: tf.Tensor(1.0, shape=(), dtype=float32)

traj[1]

BufferInfo(ids=<tf.Tensor: shape=(), dtype=int64, numpy=29>, probabilities=<tf.Tensor: shape=(), dtype=float32, numpy=0.01>)

type(traj[1])

tf_agents.replay_buffers.tf_uniform_replay_buffer.BufferInfo

traj[1]._fields

('ids', 'probabilities')

print('ids:', traj[1].ids)
print('probabilities:', traj[1].probabilities)

ids: tf.Tensor(29, shape=(), dtype=int64)
probabilities: tf.Tensor(0.01, shape=(), dtype=float32)

The agent needs access to the replay buffer. TF-Agents provide this access by creating an iterable tf.data.Dataset pipeline which will feed data to the agent.

Each row of the replay buffer only stores a single observation step. But since the DQN Agent needs both the current and next observation to compute the loss, the dataset pipeline will sample two adjacent rows for each item in the batch (num_steps=2).

The code also optimize this dataset by running parallel calls and prefetching data.

print(BATCH_SIZE)

64

# Dataset generates trajectories with shape [Bx2x...]
dataset = replay_buffer.as_dataset(
    num_parallel_calls=3, 
    sample_batch_size=BATCH_SIZE, 
    num_steps=2).prefetch(3)
dataset

<PrefetchDataset shapes: (Trajectory(step_type=(64, 2), observation=(64, 2, 4), action=(64, 2), policy_info=(), next_step_type=(64, 2), reward=(64, 2), discount=(64, 2)), BufferInfo(ids=(64, 2), probabilities=(64,))), types: (Trajectory(step_type=tf.int32, observation=tf.float32, action=tf.int64, policy_info=(), next_step_type=tf.int32, reward=tf.float32, discount=tf.float32), BufferInfo(ids=tf.int64, probabilities=tf.float32))>

iterator = iter(dataset)
print(iterator)

<tensorflow.python.data.ops.iterator_ops.OwnedIterator object at 0x7f1bd414a710>

11. Training the agent

Two things must happen during the training loop:

• collect data from the environment
• use that data to train the agent’s neural network(s)

This example also periodicially evaluates the policy and prints the current score.

The following will take ~5 minutes to run.

NUM_ITERATIONS
# NUM_ITERATIONS = 20000

20000

#@test {"skip": true}
try:
  %%time
except:
  pass

# (Optional) Optimize by wrapping some of the code in a graph using TF function.
agent.train = common.function(agent.train)

# Reset the train step
agent.train_step_counter.assign(0)

# Evaluate the agent's policy once before training.
avg_return = compute_avg_return(eval_env, agent.policy, NUM_EVAL_EPISODES)
returns = [avg_return]

for _ in range(NUM_ITERATIONS):
  # Collect a few steps using collect_policy and save to the replay buffer
  collect_data(train_env, agent.collect_policy, replay_buffer, COLLECT_STEPS_PER_ITERATION)

  # Sample a batch of data from the buffer and update the agent's network
  experience, unused_info = next(iterator)
  train_loss = agent.train(experience).loss

  step = agent.train_step_counter.numpy()

  if step % LOG_INTERVAL == 0:
    print(f'step = {step}: loss = {train_loss}')

  if step % EVAL_INTERVAL == 0:
    avg_return = compute_avg_return(eval_env, agent.policy, NUM_EVAL_EPISODES)
    print(f'step = {step}: Average Return = {avg_return}')
    returns.append(avg_return)

CPU times: user 3 µs, sys: 0 ns, total: 3 µs
Wall time: 6.44 µs
step = 200: loss = 5.8472771644592285
step = 400: loss = 6.1065521240234375
step = 600: loss = 30.35647964477539
step = 800: loss = 51.443580627441406
step = 1000: loss = 8.111553192138672
step = 1000: Average Return = 42.0
step = 1200: loss = 15.172381401062012
step = 1400: loss = 3.481518507003784
step = 1600: loss = 48.250511169433594
step = 1800: loss = 23.229551315307617
step = 2000: loss = 22.171497344970703
step = 2000: Average Return = 21.399999618530273
step = 2200: loss = 19.5601806640625
step = 2400: loss = 16.358232498168945
step = 2600: loss = 3.6557135581970215
step = 2800: loss = 44.43617630004883
step = 3000: loss = 47.758426666259766
step = 3000: Average Return = 40.900001525878906
step = 3200: loss = 5.233551025390625
step = 3400: loss = 9.2518310546875
step = 3600: loss = 54.544185638427734
step = 3800: loss = 72.3006820678711
step = 4000: loss = 21.375141143798828
step = 4000: Average Return = 63.0
step = 4200: loss = 41.15625
step = 4400: loss = 7.214105129241943
step = 4600: loss = 108.88253784179688
step = 4800: loss = 40.52140808105469
step = 5000: loss = 37.4377326965332
step = 5000: Average Return = 83.4000015258789
step = 5200: loss = 120.3891372680664
step = 5400: loss = 11.245302200317383
step = 5600: loss = 30.03839683532715
step = 5800: loss = 64.23017883300781
step = 6000: loss = 48.6501579284668
step = 6000: Average Return = 144.0
step = 6200: loss = 68.4277114868164
step = 6400: loss = 19.68730926513672
step = 6600: loss = 45.68647384643555
step = 6800: loss = 72.20692443847656
step = 7000: loss = 9.852011680603027
step = 7000: Average Return = 164.3000030517578
step = 7200: loss = 10.033541679382324
step = 7400: loss = 198.07725524902344
step = 7600: loss = 137.63177490234375
step = 7800: loss = 223.62005615234375
step = 8000: loss = 198.0550994873047
step = 8000: Average Return = 178.39999389648438
step = 8200: loss = 198.30099487304688
step = 8400: loss = 14.453493118286133
step = 8600: loss = 343.4920349121094
step = 8800: loss = 425.3981018066406
step = 9000: loss = 17.297143936157227
step = 9000: Average Return = 185.5
step = 9200: loss = 137.6107635498047
step = 9400: loss = 342.56634521484375
step = 9600: loss = 21.620716094970703
step = 9800: loss = 236.54286193847656
step = 10000: loss = 246.3893280029297
step = 10000: Average Return = 193.60000610351562
step = 10200: loss = 343.26153564453125
step = 10400: loss = 471.0173645019531
step = 10600: loss = 394.5465087890625
step = 10800: loss = 763.190673828125
step = 11000: loss = 503.9163513183594
step = 11000: Average Return = 192.10000610351562
step = 11200: loss = 1509.2169189453125
step = 11400: loss = 29.37891387939453
step = 11600: loss = 1267.962158203125
step = 11800: loss = 29.946744918823242
step = 12000: loss = 27.069908142089844
step = 12000: Average Return = 187.10000610351562
step = 12200: loss = 238.68295288085938
step = 12400: loss = 796.3482055664062
step = 12600: loss = 39.77373504638672
step = 12800: loss = 21.331676483154297
step = 13000: loss = 25.075672149658203
step = 13000: Average Return = 200.0
step = 13200: loss = 34.978187561035156
step = 13400: loss = 23.596893310546875
step = 13600: loss = 599.0440673828125
step = 13800: loss = 43.91310501098633
step = 14000: loss = 1782.3662109375
step = 14000: Average Return = 200.0
step = 14200: loss = 53.496665954589844
step = 14400: loss = 1896.657958984375
step = 14600: loss = 82.78473663330078
step = 14800: loss = 305.4472351074219
step = 15000: loss = 2803.62109375
step = 15000: Average Return = 200.0
step = 15200: loss = 756.8356323242188
step = 15400: loss = 568.4160766601562
step = 15600: loss = 3161.003662109375
step = 15800: loss = 4912.7490234375
step = 16000: loss = 59.62199020385742
step = 16000: Average Return = 200.0
step = 16200: loss = 61.728878021240234
step = 16400: loss = 742.1744995117188
step = 16600: loss = 48.09772491455078
step = 16800: loss = 1085.0491943359375
step = 17000: loss = 90.4552001953125
step = 17000: Average Return = 200.0
step = 17200: loss = 1004.1065673828125
step = 17400: loss = 1123.6953125
step = 17600: loss = 123.3787841796875
step = 17800: loss = 49.843048095703125
step = 18000: loss = 3538.21484375
step = 18000: Average Return = 200.0
step = 18200: loss = 110.32475280761719
step = 18400: loss = 3539.767578125
step = 18600: loss = 83.17483520507812
step = 18800: loss = 70.70829010009766
step = 19000: loss = 92.60458374023438
step = 19000: Average Return = 200.0
step = 19200: loss = 1833.579833984375
step = 19400: loss = 4391.30322265625
step = 19600: loss = 626.9679565429688
step = 19800: loss = 121.67256164550781
step = 20000: loss = 118.2735366821289
step = 20000: Average Return = 200.0

Visualization

Plots

Use matplotlib.pyplot to chart how the policy improved during training.

One iteration of Cartpole-v0 consists of 200 time steps. The environment gives a reward of +1 for each step the pole stays up, so the maximum return for one episode is 200. The charts shows the return increasing towards that maximum each time it is evaluated during training. (It may be a little unstable and not increase monotonically each time.)

#@test {"skip": true}
iterations = range(0, NUM_ITERATIONS + 1, EVAL_INTERVAL)
plt.plot(iterations, returns)
plt.ylabel('Average Return')
plt.xlabel('Iterations')
plt.ylim(top=250)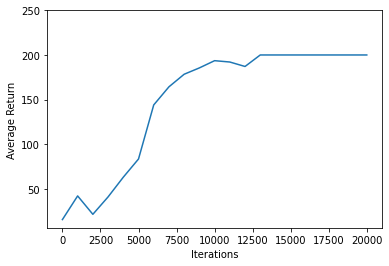

Videos

Charts are nice. But more exciting is seeing an agent actually performing a task in an environment.

First, create a function to embed videos in the notebook.

def embed_mp4(filename):
  """Embeds an mp4 file in the notebook."""
  video = open(filename,'rb').read()
  b64 = base64.b64encode(video)
  tag = '''
  <video width="640" height="480" controls>
    <source src="data:video/mp4;base64,{0}" type="video/mp4">
  Your browser does not support the video tag.
  </video>'''.format(b64.decode())

  return IPython.display.HTML(tag)

Now iterate through a few episodes of the Cartpole game with the agent. The underlying Python environment (the one “inside” the TensorFlow environment wrapper) provides a render() method, which outputs an image of the environment state. These can be collected into a video.

# def create_policy_eval_video(policy, filename, num_episodes=5, fps=30):
def create_policy_eval_video(policy, filename, num_episodes=3, fps=30):
  filename = filename + ".mp4"
  with imageio.get_writer(filename, fps=fps) as video:
    for _ in range(num_episodes):
      time_step = eval_env.reset()
      video.append_data(eval_py_env.render())
      while not time_step.is_last():
        action_step = policy.action(time_step)
        time_step = eval_env.step(action_step.action)
        video.append_data(eval_py_env.render())
  return embed_mp4(filename)

create_policy_eval_video(agent.policy, "trained-agent")

WARNING:root:IMAGEIO FFMPEG_WRITER WARNING: input image is not divisible by macro_block_size=16, resizing from (400, 600) to (400, 608) to ensure video compatibility with most codecs and players. To prevent resizing, make your input image divisible by the macro_block_size or set the macro_block_size to None (risking incompatibility). You may also see a FFMPEG warning concerning speedloss due to data not being aligned.

For fun, compare the trained agent (above) to an agent moving randomly. (It does not do as well.)

create_policy_eval_video(random_policy, "random-agent")

WARNING:root:IMAGEIO FFMPEG_WRITER WARNING: input image is not divisible by macro_block_size=16, resizing from (400, 600) to (400, 608) to ensure video compatibility with most codecs and players. To prevent resizing, make your input image divisible by the macro_block_size or set the macro_block_size to None (risking incompatibility). You may also see a FFMPEG warning concerning speedloss due to data not being aligned.