Monte Carlo 2 – Estimation of the Action-value Function in Reinforcement Learning

Find action values under a given policy

Reinforcement Learning
MC
OpenAI Gym
Author

Kobus Esterhuysen

Published

January 19, 2022

1. Introduction

In a Markov Decision Process (Figure 1) the agent and environment interacts continuously.

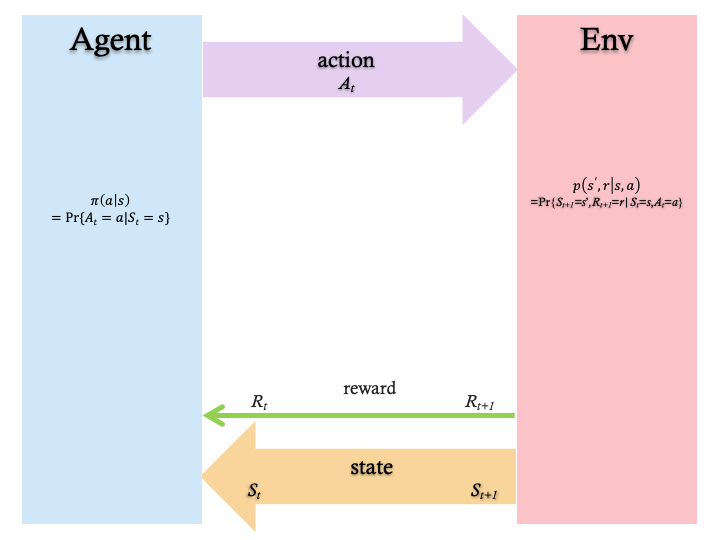
Figure 1 Agent/Environment interaction in a MDP

More details are available in Reinforcement Learning: An Introduction by Sutton and Barto.

The dynamics of the MDP is given by \[ \begin{aligned} p(s',r|s,a) &= Pr\{ S_{t+1}=s',R_{t+1}=r | S_t=s,A_t=a \} \\ \end{aligned} \]

The policy of an agent is a mapping from the current state of the environment to an action that the agent needs to take in this state. Formally, a policy is given by \[ \begin{aligned} \pi(a|s) &= Pr\{A_t=a|S_t=s\} \end{aligned} \]

The discounted return is given by \[ \begin{aligned} G_t &= R_{t+1} + \gamma R_{t+2} + \gamma ^2 R_{t+3} + ... + R_T \\ &= \sum_{k=0}^\infty \gamma ^k R_{t+1+k} \end{aligned} \] where \(\gamma\) is the discount factor and \(R\) is the reward.

Most reinforcement learning algorithms involve the estimation of value functions - in our present case, the state-value function. The state-value function maps each state to a measure of “how good it is to be in that state” in terms of expected rewards. Formally, the state-value function, under policy \(\pi\) is given by \[ \begin{aligned} v_\pi(s) &= \mathbb{E}_\pi[G_t|S_t=s] \end{aligned} \]

The Monte Carlo algorithm discussed in this post will numerically estimate \(v_\pi(s)\).

2. Environment

The environment is the game of Blackjack. The player tries to get cards whose sum is as great as possible without exceeding 21. Face cards count as 10. An ace can be taken either as a 1 or an 11. Two cards are dealth to both dealer and player. One of the dealer’s cards is face up (other is face down). The player can request additional cards, one by one (called hits) until the player stops (called sticks) or goes above 21 (goes bust and loses). When the players sticks it becomes the dealer’s turn which uses a fixed strategy: sticks when the sum is 17 or greater and hits otherwise. If the dealer goes bust the player wins, otherwise the winner is determined by whose sum is closer to 21.

We formulate this game as an episodic finite MDP. Each game is an episode.

  • States are based on the player’s
    • current sum (12-21)
      • player will automatically keep on getting cards until the sum is at least 12 (this is a rule and the player does not have a choice in this matter)
    • dealer’s face up card (ace-10)
    • whether player holds usable ace (True or False)

This gives a total of 200 states: \(10 × 10 \times 2 = 200\)

  • Rewards:
    • +1 for winning
    • -1 for losing
    • 0 for drawing
  • Reward for stick:
    • +1 if sum > sum of dealer
    • 0 if sum = sum of dealer
    • -1 if sum < sum of dealer
  • Reward for hit:
    • -1 if sum > 21
    • 0 otherwise

The environment is implemented using the OpenAI Gym library.

3. Agent

The agent is the player. After observing the state of the environment, the agent can take one of two possible actions:

  • stick (0) [stop receiving cards]
  • hit (1) [have another card]

The agent’s policy will be deterministic - will always stick of the sum is 20 or 21, and hit otherwise. We call this policy1 in the code.

4. Monte Carlo Estimation of the Action-value Function, \(q_\pi(s,a)\)

We will now proceed to estimate the action-value function for the given policy \(\pi\). We can take \(\gamma=1\) as the sum will remain finite:

\[ \large \begin{aligned} q_\pi(s,a) &= \mathbb{E}_\pi[G_t | S_t=s, A_t=a] \\ &= \mathbb{E}_\pi[R_{t+1} + \gamma R_{t+2} + \gamma ^2 R_{t+3} + ... + R_T | S_t=s, A_t=a] \\ &= \mathbb{E}_\pi[R_{t+1} + R_{t+2} + R_{t+3} + ... + R_T | S_t=s, A_t=a] \end{aligned} \]

In numeric terms this means that, given a state and an action, we take the sum of all rewards from that state onwards (following policy \(\pi\)) until the game ends, and take the average of all such sequences.

5. Implementation

We consider two versions of the MC Prediction algorithm: A forward version, and a backward version.

Figure 2 shows the forward version:

Figure 2 First-visit MC Prediction (forward), for estimating Q

Figure 3 shows the backward version:

Figure 3 First-visit MC Prediction (backard), for estimating Q

Next, we present the code that implements the algorithm.

import gym
import matplotlib
import numpy as np
import sys
from collections import defaultdict
import pprint as pp
from matplotlib import pyplot as plt
%matplotlib inline
# hide
# from lib import plotting as myplot
# from lib.envs.blackjack import BlackjackEnv
from dennybritz_lib import plotting as myplot
from dennybritz_lib.envs.blackjack import BlackjackEnv
env = BlackjackEnv()

5.1 Policy

The following function captures the policy used by the agent:

def policy1(observation):
    player_sum, dealer_showing, usable_ace = observation
    if player_sum >=20:
      return 0 #stick
    else:
      return 1 #hit

5.2 Generate episodes

The following function sets the environment to a random initial state. It then enters a loop where each iteration applies the policy to the environment’s state to obtain the next action to be taken by the agent. That action is then applied to the environment to get the next state, and so on until the episode ends.

def generate_episode(env, policy):
  episode = []
  state = env.reset() #to a random state
  action = np.random.choice([0, 1]) #to a random action, for exploring starts
  while True:
      # action = policy(state)
      next_state, reward, done, _ = env.step(action) # St+1, Rt+1 OR s',r
      episode.append((state, action, reward)) # St, At, Rt+1 OR s,a,r
      if done:
          break
      state = next_state
      action = policy(state)
  return episode

5.3 Main loop

The following function implements the main loop of the algorithm. It iterates for n_episodes. It also takes a list of monitored_state_actions for which it will record the evolution of action values. This is handy for showing how action values converge during the process.

5.3.1 First-Visit Forward Algorithm

def first_visit_forward_algorithm(episode, G_sum, G_cnt, Q, discount_factor, diag):
  # Find all visited state-actions in this episode
  episode_state_actions = set([(tuple(sar[0]), sar[1]) for sar in episode]); print(f'-episode_state_actions: {episode_state_actions}') if diag else None
  for state,action in episode_state_actions: #don't use St,At, they come from set, time seq not relevant
    state_action = (state, action)
    #--find the first visit to the state_action in the episode
    # first_visit_ix = next(i for i,sar in enumerate(episode) if sar[0]==state and sar[1]==action)
    visit_ixs = [i for i,sar in enumerate(episode) if sar[0]==state and sar[1]==action]; print(f'---state_action {state_action} visit_ixs: {visit_ixs}') if diag else None
    first_visit_ix = visit_ixs[0]; print(f"first_visit_ix: {first_visit_ix}") if diag else None
    #--sum up all rewards since the first visit
    print(f"episode[first_visit_ix:]: {episode[first_visit_ix:]}") if diag else None
    print(f"rewards: {[sar[2]*(discount_factor**i) for i,sar in enumerate(episode[first_visit_ix:])]}") if diag else None
    G = sum([sar[2]*(discount_factor**i) for i,sar in enumerate(episode[first_visit_ix:])]); print(f"G: {G}") if diag else None
    #--average return for this state_action over all sampled episodes
    #--instead of appending, keep a running sum and count
    G_sum[state_action] += G; G_cnt[state_action] += 1.0
    Q[state][action] = G_sum[state_action]/G_cnt[state_action]

5.3.2 First-Visit Backward Algorithm

def first_visit_backward_algorithm(episode, G_sum, G_cnt, Q, discount_factor, diag):
  G = 0.0
  episode_state_actions = [(sar[0], sar[1]) for sar in episode]; print(f'-episode_state_actions: {episode_state_actions}') if diag else None #put St,At in tuple and use as key  
  for t in range(len(episode))[::-1]:
    St, At, Rtp1 = episode[t]
    print(f"---t={t} St, At, Rt+1: {St, At, Rtp1}") if diag else None
    G = discount_factor*G + Rtp1
    print(f"G: {G}") if diag else None
    if (St,At) not in episode_state_actions[0:t]: #S0,A0,S1,A1,...,St-1,At-1, i.e. all earlier states
      print(f"{(St,At)} not in {episode_state_actions[0:t]}, processing ...") if diag else None
      G_sum[(St,At)] += G; print(f"G_sum[(St,At)]: {G_sum[(St,At)]}") if diag else None
      G_cnt[(St,At)] += 1.0; print(f"G_cnt[(St,At)]: {G_cnt[(St,At)]}") if diag else None
      Q[St][At] = G_sum[(St,At)]/G_cnt[(St,At)]; print(f"Q[St][At]: {Q[St][At]}") if diag else None
    else:
      print(f"{(St,At)} IS in {episode_state_actions[0:t]}, skipping ...") if diag else None

5.3.3 Final First-Visit Algorithm

We decide on using the backward version from now on. It may be a bit more challenging to understand, but it provides more efficient computation. In the next function, we always call the backward version by means of the call:

first_visit_forward_algorithm(episode, G_sum, G_cnt, Q, discount_factor, diag)

def mc_estimation(env, n_episodes, discount_factor=1.0, monitored_state_actions=None, diag=False):
  G_sum = defaultdict(float)
  G_count = defaultdict(float)
  Q = defaultdict(lambda: np.zeros(env.action_space.n)) #final action-value function
  pi = policy1
  monitored_state_action_values = defaultdict(list)
  for i in range(1, n_episodes + 1):
    if i%1000 == 0: print("\rEpisode {}/{}".format(i, n_episodes), end=""); sys.stdout.flush()
    episode = generate_episode(env, pi); print(f'\nepisode {i}: {episode}') if diag else None
    # first_visit_forward_algorithm(episode, G_sum, G_cnt, Q, discount_factor, diag)
    first_visit_backward_algorithm(episode, G_sum, G_cnt, Q, discount_factor, diag)
    if monitored_state_actions:
      for msa in monitored_state_actions: 
        s = msa[0]; a = msa[1]            
        # print("\rQ[{}]: {}".format(msa, Q[s][a]), end=""); sys.stdout.flush()
        monitored_state_action_values[msa].append(Q[s][a])
  print('\n++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++') if diag else None
  pp.pprint(f'G_sum: {G_sum}') if diag else None
  pp.pprint(f'G_count: {G_count}') if diag else None
  print('++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++') if diag else None
  print('\nmonitored_state_action_values:', monitored_state_action_values) if diag else None
  return Q,monitored_state_action_values

5.4 Monitored state-actions

Let’s pick a number of state-actions to monitor. Each tuple captures the player’s sum, the dealer’s showing card, and whether the player has a usable ace, as well as the action taken in the state:

monitored_state_actions=[((21, 7, False), 0), ((20, 7, True), 0), ((12, 7, False), 1), ((17, 7, True), 0)]
Q,monitored_state_action_values = mc_estimation(
  env, 
  n_episodes=10, 
  monitored_state_actions=monitored_state_actions,
  diag=True)

episode 1: [((13, 7, False), 1, 0), ((19, 7, False), 1, 0), ((21, 7, False), 0, 1)]
-episode_state_actions: [((13, 7, False), 1), ((19, 7, False), 1), ((21, 7, False), 0)]
---t=2 St, At, Rt+1: ((21, 7, False), 0, 1)
G: 1.0
((21, 7, False), 0) not in [((13, 7, False), 1), ((19, 7, False), 1)], processing ...
G_sum[(St,At)]: 1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: 1.0
---t=1 St, At, Rt+1: ((19, 7, False), 1, 0)
G: 1.0
((19, 7, False), 1) not in [((13, 7, False), 1)], processing ...
G_sum[(St,At)]: 1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: 1.0
---t=0 St, At, Rt+1: ((13, 7, False), 1, 0)
G: 1.0
((13, 7, False), 1) not in [], processing ...
G_sum[(St,At)]: 1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: 1.0

episode 2: [((13, 4, False), 0, -1)]
-episode_state_actions: [((13, 4, False), 0)]
---t=0 St, At, Rt+1: ((13, 4, False), 0, -1)
G: -1.0
((13, 4, False), 0) not in [], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0

episode 3: [((14, 5, False), 0, -1)]
-episode_state_actions: [((14, 5, False), 0)]
---t=0 St, At, Rt+1: ((14, 5, False), 0, -1)
G: -1.0
((14, 5, False), 0) not in [], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0

episode 4: [((13, 3, False), 1, -1)]
-episode_state_actions: [((13, 3, False), 1)]
---t=0 St, At, Rt+1: ((13, 3, False), 1, -1)
G: -1.0
((13, 3, False), 1) not in [], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0

episode 5: [((16, 8, False), 0, 1)]
-episode_state_actions: [((16, 8, False), 0)]
---t=0 St, At, Rt+1: ((16, 8, False), 0, 1)
G: 1.0
((16, 8, False), 0) not in [], processing ...
G_sum[(St,At)]: 1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: 1.0

episode 6: [((20, 10, False), 0, 1)]
-episode_state_actions: [((20, 10, False), 0)]
---t=0 St, At, Rt+1: ((20, 10, False), 0, 1)
G: 1.0
((20, 10, False), 0) not in [], processing ...
G_sum[(St,At)]: 1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: 1.0

episode 7: [((20, 10, False), 1, -1)]
-episode_state_actions: [((20, 10, False), 1)]
---t=0 St, At, Rt+1: ((20, 10, False), 1, -1)
G: -1.0
((20, 10, False), 1) not in [], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0

episode 8: [((17, 10, False), 0, 1)]
-episode_state_actions: [((17, 10, False), 0)]
---t=0 St, At, Rt+1: ((17, 10, False), 0, 1)
G: 1.0
((17, 10, False), 0) not in [], processing ...
G_sum[(St,At)]: 1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: 1.0

episode 9: [((20, 10, False), 0, 0)]
-episode_state_actions: [((20, 10, False), 0)]
---t=0 St, At, Rt+1: ((20, 10, False), 0, 0)
G: 0.0
((20, 10, False), 0) not in [], processing ...
G_sum[(St,At)]: 1.0
G_cnt[(St,At)]: 2.0
Q[St][At]: 0.5

episode 10: [((17, 10, False), 1, 0), ((19, 10, False), 1, -1)]
-episode_state_actions: [((17, 10, False), 1), ((19, 10, False), 1)]
---t=1 St, At, Rt+1: ((19, 10, False), 1, -1)
G: -1.0
((19, 10, False), 1) not in [((17, 10, False), 1)], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0
---t=0 St, At, Rt+1: ((17, 10, False), 1, 0)
G: -1.0
((17, 10, False), 1) not in [], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0

++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
("G_sum: defaultdict(<class 'float'>, {((21, 7, False), 0): 1.0, ((19, 7, "
 'False), 1): 1.0, ((13, 7, False), 1): 1.0, ((13, 4, False), 0): -1.0, ((14, '
 '5, False), 0): -1.0, ((13, 3, False), 1): -1.0, ((16, 8, False), 0): 1.0, '
 '((20, 10, False), 0): 1.0, ((20, 10, False), 1): -1.0, ((17, 10, False), 0): '
 '1.0, ((19, 10, False), 1): -1.0, ((17, 10, False), 1): -1.0})')
"G_count: defaultdict(<class 'float'>, {})"
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

monitored_state_action_values: defaultdict(<class 'list'>, {((21, 7, False), 0): [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0], ((20, 7, True), 0): [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], ((12, 7, False), 1): [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], ((17, 7, True), 0): [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]})
Q
defaultdict(<function __main__.mc_estimation.<locals>.<lambda>>,
            {(12, 7, False): array([0., 0.]),
             (13, 3, False): array([ 0., -1.]),
             (13, 4, False): array([-1.,  0.]),
             (13, 7, False): array([0., 1.]),
             (14, 5, False): array([-1.,  0.]),
             (16, 8, False): array([1., 0.]),
             (17, 7, True): array([0., 0.]),
             (17, 10, False): array([ 1., -1.]),
             (19, 7, False): array([0., 1.]),
             (19, 10, False): array([ 0., -1.]),
             (20, 7, True): array([0., 0.]),
             (20, 10, False): array([ 0.5, -1. ]),
             (21, 7, False): array([1., 0.])})
Q[(13, 5, False)]
array([0., 0.])
Q[(13, 5, False)][0], Q[(13, 5, False)][1]
(0.0, 0.0)
print(monitored_state_actions[0])
print(monitored_state_action_values[monitored_state_actions[0]])
((21, 7, False), 0)
[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0]
# last value in monitored_state_actions should be value in Q
msa = monitored_state_actions[0]; print('msa:', msa)
s = msa[0]; print('s:', s)
a = msa[1]; print('a:', a)
monitored_state_action_values[msa][-1], Q[s][a] #monitored_stuff[msa] BUT Q[s][a]
msa: ((21, 7, False), 0)
s: (21, 7, False)
a: 0
(1.0, 1.0)

5.5 Run 1

First, we will run the algorithm for 10,000 episodes, using policy1:

Q1,monitored_state_action_values1 = mc_estimation(
    env, 
    n_episodes=10_000, 
    monitored_state_actions=monitored_state_actions,
    diag=False)
Episode 10000/10000
# last value in monitored_state_actions should be value in Q
msa = monitored_state_actions[0]; print('msa:', msa)
s = msa[0]; print('s:', s)
a = msa[1]; print('a:', a)
monitored_state_action_values1[msa][-1], Q1[s][a] #monitored_stuff[msa] BUT Q[s][a]
msa: ((21, 7, False), 0)
s: (21, 7, False)
a: 0
(0.925, 0.925)

The following chart shows how the values of the 4 monitored state-actions converge to their values:

plt.rcParams["figure.figsize"] = (18,10)
for msa in monitored_state_actions:
  plt.plot(monitored_state_action_values1[msa])
plt.title('Estimated $q_\pi(s,a)$ for some state-actions', fontsize=18)
plt.xlabel('Episodes', fontsize=16)
plt.ylabel('Estimated $q_\pi(s,a)$', fontsize=16)
plt.legend(monitored_state_actions, fontsize=16)
plt.show()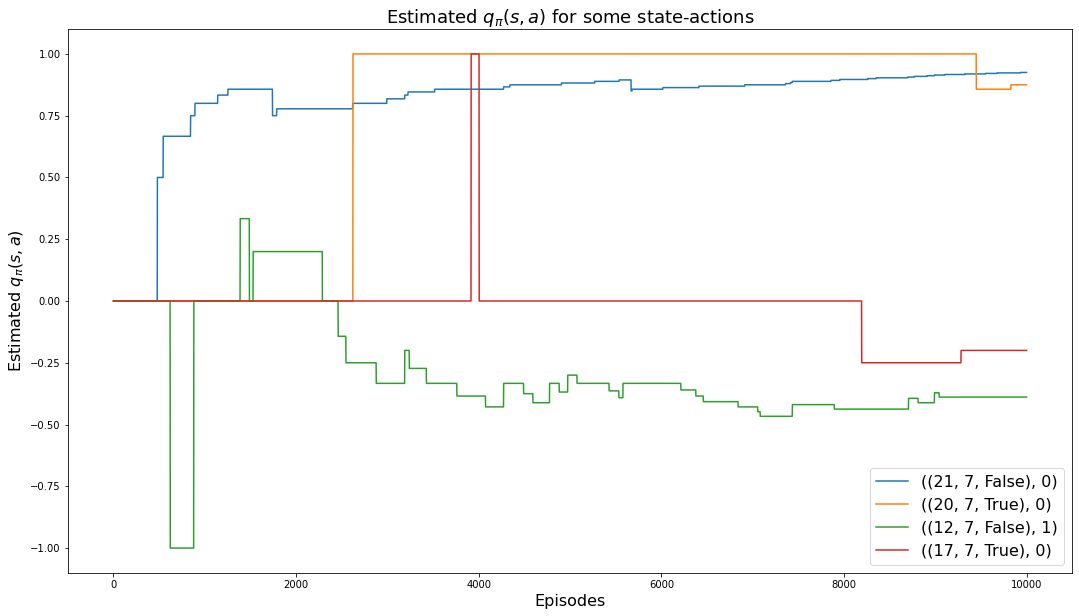

The following wireframe charts shows the estimate of the action-value function, \(q_\pi(s,a)\), for the cases of a usable ace as well as not a usable ace:

AZIM = -110
ELEV = 20
myplot.plot_action_value_function(Q1, title="10,000 Steps", wireframe=True, azim=AZIM, elev=ELEV)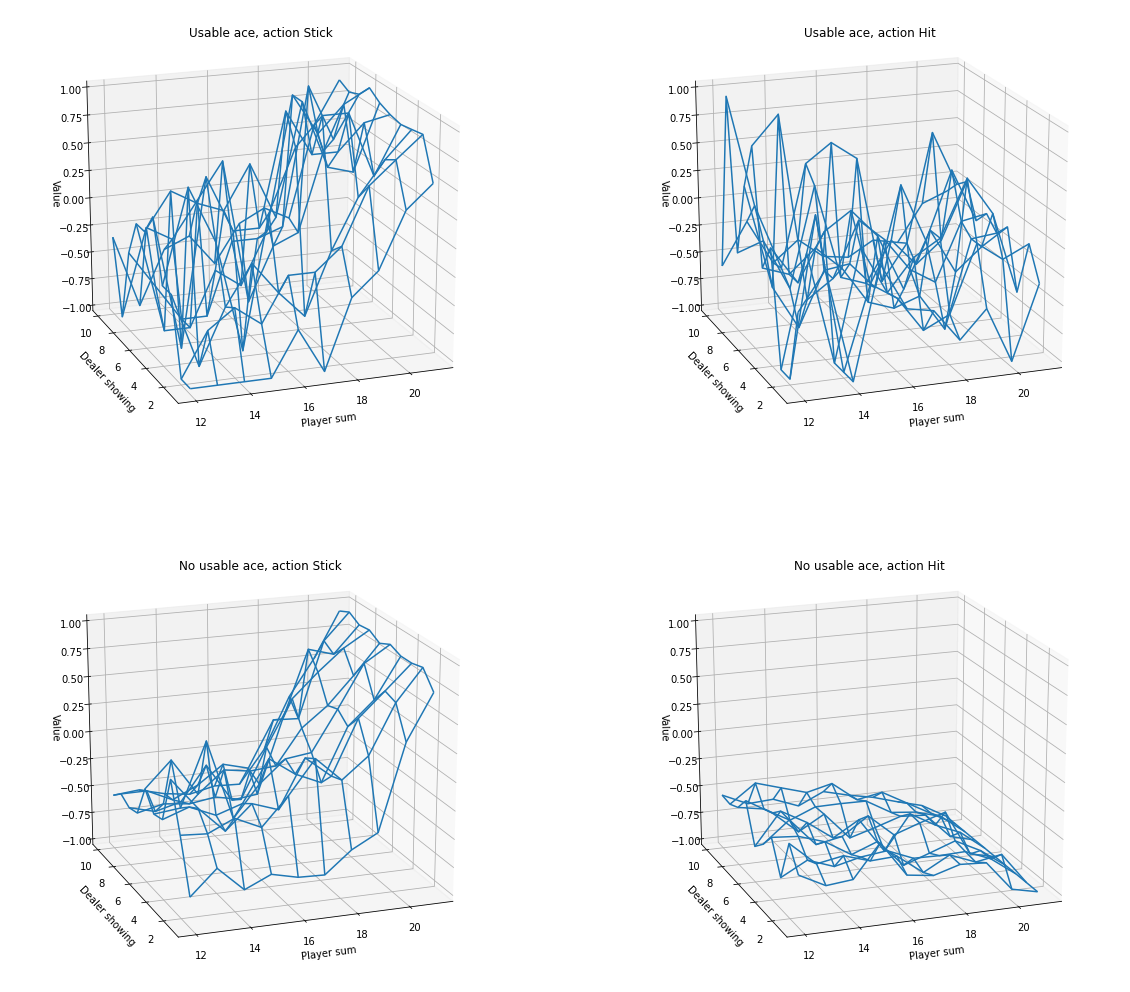

Here are the same charts but with coloration:

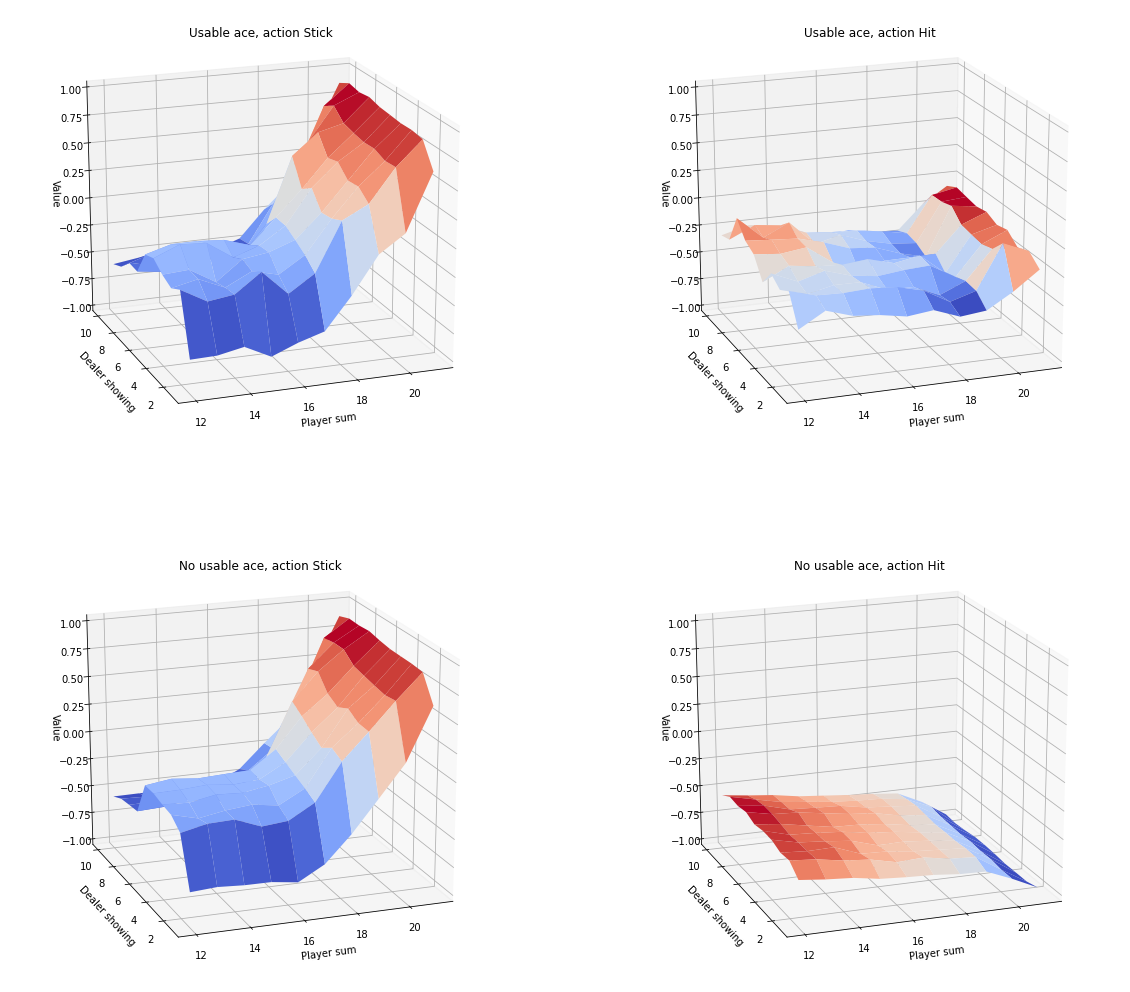
myplot.plot_action_value_function(Q1, title="10,000 Steps", wireframe=False, azim=AZIM, elev=ELEV)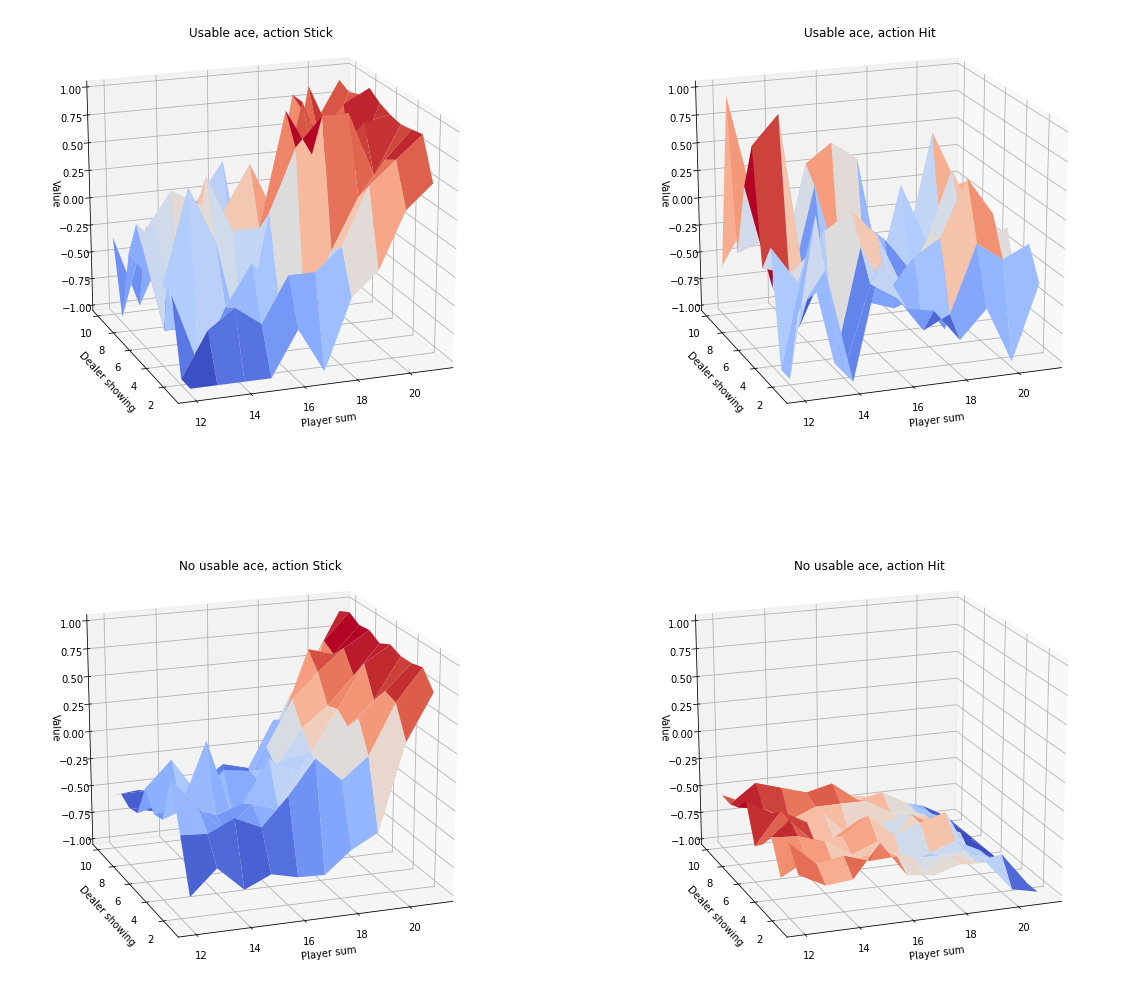

5.6 Run 2

Our final run uses 500,000 episodes and the accuracy of the action-value function is higher.

Q2,monitored_state_action_values2 = mc_estimation(
    env, 
    n_episodes=500_000, 
    monitored_state_actions=monitored_state_actions,
    diag=False)
Episode 500000/500000
# last value in monitored_state_actions should be value in Q
msa = monitored_state_actions[0]; print('msa:', msa)
s = msa[0]; print('s:', s)
a = msa[1]; print('a:', a)
monitored_state_action_values2[msa][-1], Q2[s][a] #monitored_stuff[msa] BUT Q[s][a]
msa: ((21, 7, False), 0)
s: (21, 7, False)
a: 0
(0.9148, 0.9148)
plt.rcParams["figure.figsize"] = (18,12)
for msa in monitored_state_actions:
  plt.plot(monitored_state_action_values2[msa])
plt.title('Estimated $q_\pi(s,a)$ for some state-actions', fontsize=18)
plt.xlabel('Episodes', fontsize=16)
plt.ylabel('Estimated $q_\pi(s,a)$', fontsize=16)
plt.legend(monitored_state_actions, fontsize=16)
plt.show()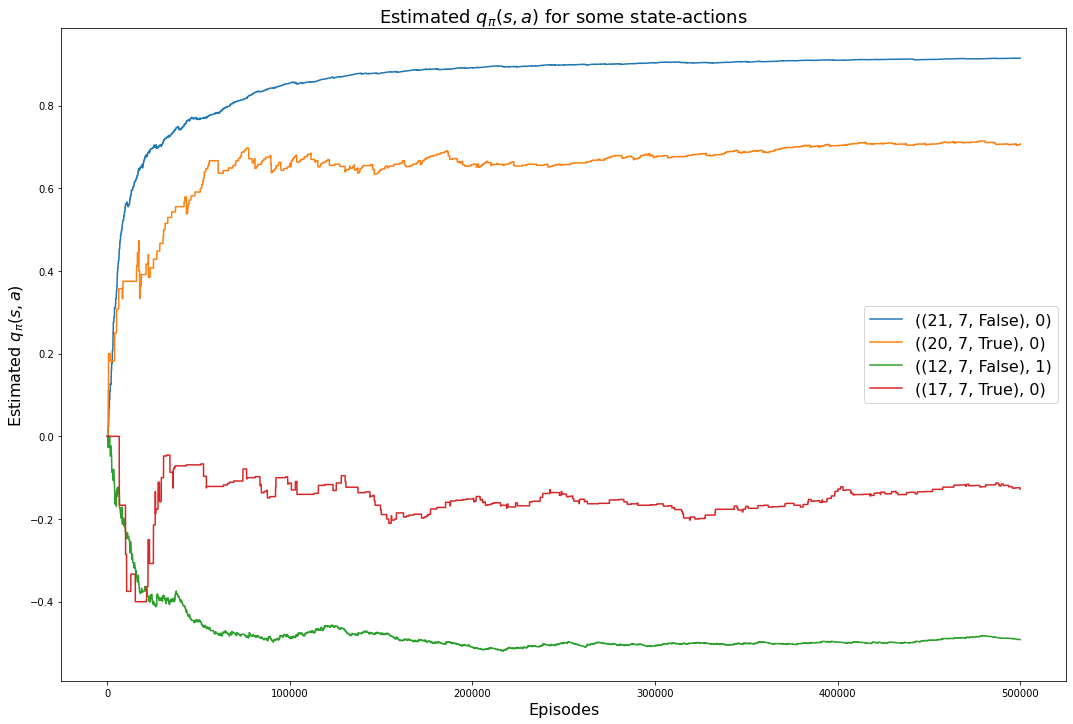

myplot.plot_action_value_function(Q2, title="500,000 Steps", wireframe=True, azim=AZIM, elev=ELEV)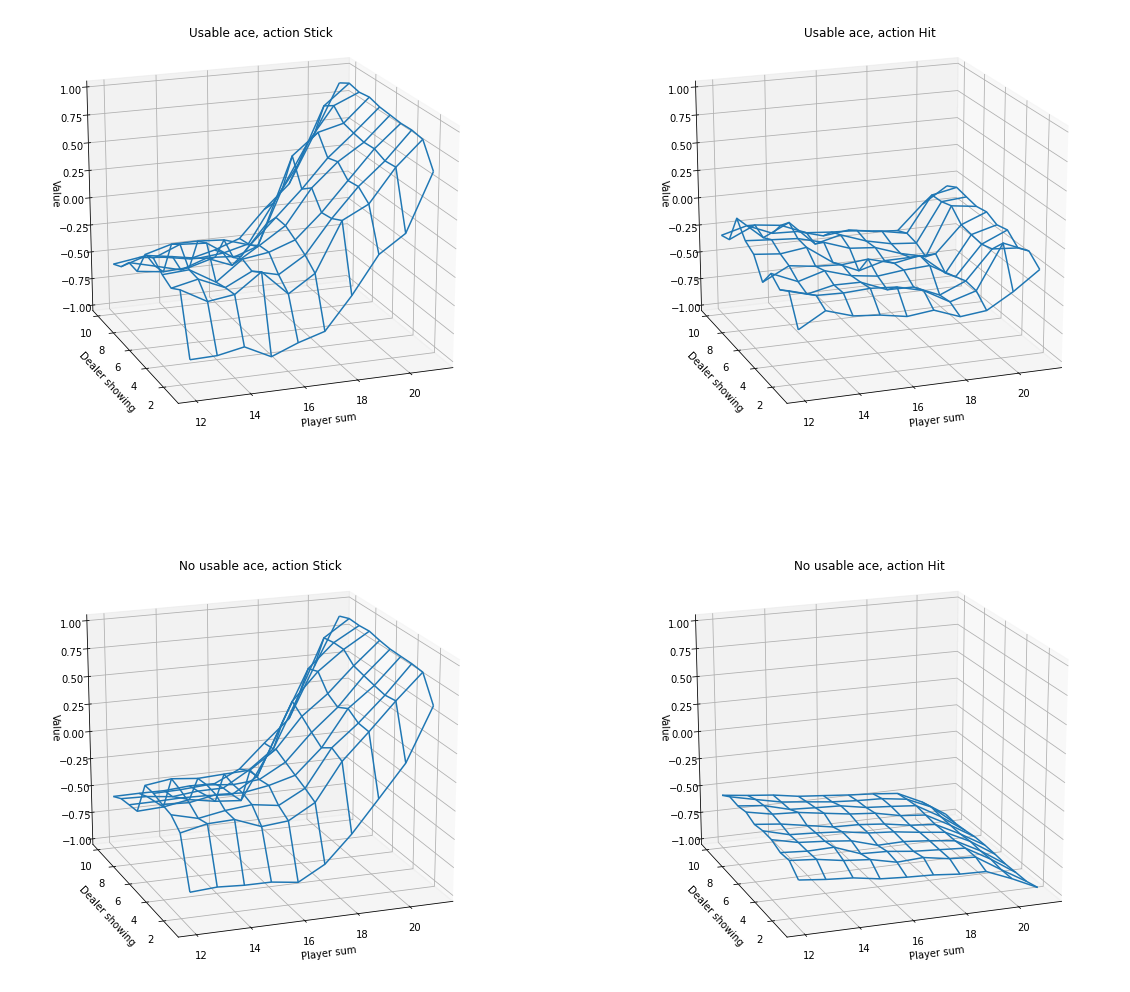

myplot.plot_action_value_function(Q2, title="500,000 Steps", wireframe=False, azim=AZIM, elev=ELEV)