import gym
import matplotlib
import numpy as np
import sys
from collections import defaultdict
import pprint as pp
from matplotlib import pyplot as plt
%matplotlib inline1. Introduction
In a Markov Decision Process (Figure 1) the agent and environment interacts continuously.
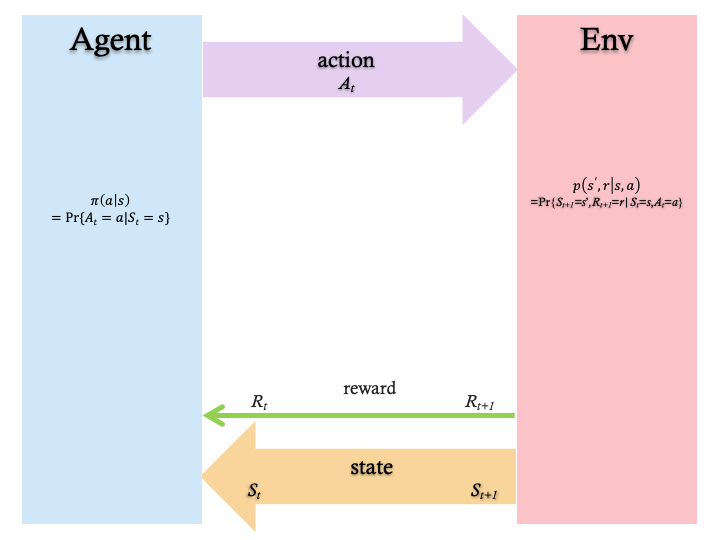
More details are available in Reinforcement Learning: An Introduction by Sutton and Barto.
The dynamics of the MDP is given by \[ \begin{aligned} p(s',r|s,a) &= Pr\{ S_{t+1}=s',R_{t+1}=r | S_t=s,A_t=a \} \\ \end{aligned} \]
The policy of an agent is a mapping from the current state of the environment to an action that the agent needs to take in this state. Formally, a policy is given by \[ \begin{aligned} \pi(a|s) &= Pr\{A_t=a|S_t=s\} \end{aligned} \]
The discounted return is given by \[ \begin{aligned} G_t &= R_{t+1} + \gamma R_{t+2} + \gamma ^2 R_{t+3} + ... + R_T \\ &= \sum_{k=0}^\infty \gamma ^k R_{t+1+k} \end{aligned} \] where \(\gamma\) is the discount factor and \(R\) is the reward.
Most reinforcement learning algorithms involve the estimation of value functions - in our present case, the state-value function. The state-value function maps each state to a measure of “how good it is to be in that state” in terms of expected rewards. Formally, the state-value function, under policy \(\pi\) is given by \[ \begin{aligned} v_\pi(s) &= \mathbb{E}_\pi[G_t|S_t=s] \end{aligned} \]
The Monte Carlo algorithm discussed in this post will numerically estimate \(v_\pi(s)\).
2. Environment
The environment is the game of Blackjack. The player tries to get cards whose sum is as great as possible without exceeding 21. Face cards count as 10. An ace can be taken either as a 1 or an 11. Two cards are dealth to both dealer and player. One of the dealer’s cards is face up (other is face down). The player can request additional cards, one by one (called hits) until the player stops (called sticks) or goes above 21 (goes bust and loses). When the players sticks it becomes the dealer’s turn which uses a fixed strategy: sticks when the sum is 17 or greater and hits otherwise. If the dealer goes bust the player wins, otherwise the winner is determined by whose sum is closer to 21.
We formulate this game as an episodic finite MDP. Each game is an episode.
- States are based on the player’s
- current sum (12-21)
- player will automatically keep on getting cards until the sum is at least 12 (this is a rule and the player does not have a choice in this matter)
- dealer’s face up card (ace-10)
- whether player holds usable ace (True or False)
- current sum (12-21)
This gives a total of 200 states: \(10 × 10 \times 2 = 200\)
- Rewards:
- +1 for winning
- -1 for losing
- 0 for drawing
- Reward for stick:
- +1 if sum > sum of dealer
- 0 if sum = sum of dealer
- -1 if sum < sum of dealer
- Reward for hit:
- -1 if sum > 21
- 0 otherwise
The environment is implemented using the OpenAI Gym library.
3. Agent
The agent is the player. After observing the state of the environment, the agent can take one of two possible actions:
- stick (0) [stop receiving cards]
- hit (1) [have another card]
The agent’s policy will be deterministic - will always stick of the sum is 20 or 21, and hit otherwise. We call this policy1 in the code.
4. Monte Carlo Control with Exploring Starts
We will now proceed to show how the estimation of the action-value function can be used in control. In other words, we want to obtain optimal policies that an agent (or controller) can use. By making use of the principle of genralized policy iteration (GPI) we maintain both an approximate policy and an approximate action-value function. During this process the action-value function is repeatedly altered to more closely appoximate the action-value function for the current policy (policy evaluation), and the policy is repeatedly improved with respect to the current action-value function (policy improvement). Creating a moving target for the other, these two kinds of changes tend to work against each other. However, together they cause both the policy and the action-value function to approach optimality.
There is a complication, however, in that many state-action pairs may never be visited. One way to address this problem is to specify that each episode starts in a state-action pair and that every pair has a nonzero probability of being selected as the starting state-action pair. In the limit this ensures that all state-action pairs will be visited an infinite number of times as the number of episodes go to infinity. This is the assumption of exploring starts.
Policy improvement is accomplished by making the policy greedy with respect to the value function. For any action-value function \(q\), the corresponding greedy policy is the one that, for each \(s ∈ \mathcal{S}\), deterministically chooses an action with the maximal action-value:
\[ \large \begin{aligned} \pi(s) &= arg max_a q(s,a) \\ \end{aligned} \]
In Monte Carlo policy iteration we alternate between policy evaluation and policy improvement on an episode-by-episode basis. After each episode, the returns are used for policy evaluation, i.e. to update the value of \(q(s,a)\) for all the visited state-actions in the episode. Then the policy is improved at all the visited states in the episode. We use the Monte Carlo ES here to estimate \(\pi_*\)(ES stands for Exploring Starts).
5. Implementation
We consider two versions of the MC Prediction algorithm: A forward version, and a backward version.
Figure 2 shows the forward version:
Figure 3 shows the backward version:
Next, we present the code that implements the algorithm.
env = BlackjackEnv()5.1 Policy
The optimal policy \(\pi_*\) is estimated with the Monte Carlo ES algorithm:
5.2 Generate episodes
The following function sets the environment to a random initial state. After that a random action is selected. These two steps ensure the exploring starts assumption. It then enters a loop where each iteration applies the current version of the policy pi to the environment’s state to obtain the next action to be taken by the agent. That action is then applied to the environment to get the next state, and so on until the episode ends.
def generate_episode(env, policy):
episode = []
state = env.reset() #to a random state
action = np.random.choice([0, 1]) #to a random action, for exploring starts
while True:
# action = policy(state)
next_state, reward, done, _ = env.step(action) # St+1, Rt+1 OR s',r
episode.append((state, action, reward)) # St, At, Rt+1 OR s,a,r
if done:
break
state = next_state
# action = policy(state)
action = policy[state]
return episode5.3 Main loop
The following function initializes the policy \(\pi\) before the algorithm’s main loop is entered. For each state \(s\), a random value is chosen from [0, 1].
def create_policy():
policy = defaultdict(int)
for sum in [12, 13, 14, 15, 16, 17, 18, 19, 20, 21]:
for showing in [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]:
for usable in [False, True]:
policy[(sum, showing, usable)] = np.random.choice([0, 1]) #random
# policy[(sum, showing, usable)] = 0 #all zeros
return policyThe following function implements the main loop of the algorithm. It iterates for n_episodes. It also takes a list of monitored_state_actions for which it will record the evolution of action values. This is handy for showing how action values converge during the process.
5.3.1 First-Visit Forward Algorithm
def first_visit_forward_algorithm(episode, G_sum, G_cnt, Q, pi, discount_factor, diag):
# Find all visited state-actions in this episode
episode_state_actions = set([(tuple(sar[0]), sar[1]) for sar in episode]); print(f'-episode_state_actions: {episode_state_actions}') if diag else None
for state,action in episode_state_actions: #don't use St,At, they come from set, time seq not relevant
state_action = (state, action)
#--find the first visit to the state_action in the episode
# first_visit_ix = next(i for i,sar in enumerate(episode) if sar[0]==state and sar[1]==action)
visit_ixs = [i for i,sar in enumerate(episode) if sar[0]==state and sar[1]==action]; print(f'---state_action {state_action} visit_ixs: {visit_ixs}') if diag else None
first_visit_ix = visit_ixs[0]; print(f"first_visit_ix: {first_visit_ix}") if diag else None
#--sum up all rewards since the first visit
print(f"episode[first_visit_ix:]: {episode[first_visit_ix:]}") if diag else None
print(f"rewards: {[sar[2]*(discount_factor**i) for i,sar in enumerate(episode[first_visit_ix:])]}") if diag else None
G = sum([sar[2]*(discount_factor**i) for i,sar in enumerate(episode[first_visit_ix:])]); print(f"G: {G}") if diag else None
# Policy Evaluation (requires exploration)
#--average return for this state_action over all sampled episodes
#--instead of appending, keep a running sum and count
G_sum[state_action] += G; G_cnt[state_action] += 1.0
Q[state][action] = G_sum[state_action]/G_cnt[state_action]
# Policy Improvement (requires exploitation)
A_star = np.argmax(Q[state]) #greedify pi, max_a Q[state][0], Q[state][1]
pi[state] = A_star5.3.2 First-Visit Backward Algorithm
def first_visit_backward_algorithm(episode, G_sum, G_cnt, Q, pi, discount_factor, diag):
G = 0.0
episode_state_actions = [(sar[0], sar[1]) for sar in episode]; print(f'-episode_state_actions: {episode_state_actions}') if diag else None #put St,At in tuple and use as key
for t in range(len(episode))[::-1]:
St, At, Rtp1 = episode[t]
print(f"---t={t} St, At, Rt+1: {St, At, Rtp1}") if diag else None
G = discount_factor*G + Rtp1
print(f"G: {G}") if diag else None
if (St,At) not in episode_state_actions[0:t]: #S0,A0,S1,A1,...,St-1,At-1, i.e. all earlier states
print(f"{(St,At)} not in {episode_state_actions[0:t]}, processing ...") if diag else None
# Policy Evaluation (requires exploration)
G_sum[(St,At)] += G; print(f"G_sum[(St,At)]: {G_sum[(St,At)]}") if diag else None
G_cnt[(St,At)] += 1.0; print(f"G_cnt[(St,At)]: {G_cnt[(St,At)]}") if diag else None
Q[St][At] = G_sum[(St,At)]/G_cnt[(St,At)]; print(f"Q[St][At]: {Q[St][At]}") if diag else None
# Policy Improvement (requires exploitation)
A_star = np.argmax(Q[St]) #greedify pi, max_a Q[state][0], Q[state][1]
pi[St] = A_star
else:
print(f"{(St,At)} IS in {episode_state_actions[0:t]}, skipping ...") if diag else None5.3.3 Final First-Visit Control Algorithm
We decide on using the backward version from now on. It may be a bit more challenging to understand, but it provides more efficient computation. In the next function, we always call the backward version by means of the call:
first_visit_backward_algorithm(episode, G_sum, G_cnt, Q, pi, discount_factor, diag)
def mc_control(env, n_episodes, discount_factor=1.0, monitored_state_actions=None, diag=False):
G_sum = defaultdict(float)
G_cnt = defaultdict(float)
Q = defaultdict(lambda: np.zeros(env.action_space.n)) #final action-value function
# policy = policy1
pi = create_policy() #policy to be optimized
monitored_state_action_values = defaultdict(list)
# monitored_pi_values = defaultdict(list)
for i in range(1, n_episodes + 1):
if i%1000 == 0: print("\rEpisode {}/{}".format(i, n_episodes), end=""); sys.stdout.flush()
# Policy Evaluation (requires exploration)
episode = generate_episode(env, pi); print(f'\nepisode {i}: {episode}') if diag else None
# first_visit_forward_algorithm(episode, G_sum, G_cnt, Q, pi, discount_factor, diag)
first_visit_backward_algorithm(episode, G_sum, G_cnt, Q, pi, discount_factor, diag)
if monitored_state_actions:
for msa in monitored_state_actions:
s = msa[0]; a = msa[1]
# print("\rQ[{}]: {}".format(msa, Q[s][a]), end=""); sys.stdout.flush()
monitored_state_action_values[msa].append(Q[s][a])
# monitored_pi_values[s].append(pi[state])
print('\n++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++') if diag else None
pp.pprint(f'G_sum: {G_sum}') if diag else None
pp.pprint(f'G_cnt: {G_cnt}') if diag else None
print('++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++') if diag else None
print('\nmonitored_state_action_values:', monitored_state_action_values) if diag else None
# return Q,pi,monitored_state_action_values,monitored_pi_values
return Q,pi,monitored_state_action_values5.4 Monitored state-actions
Let’s pick a number of state-actions to monitor. Each tuple captures the player’s sum, the dealer’s showing card, and whether the player has a usable ace, as well as the action taken in the state:
monitored_state_actions=[((21, 7, False), 0), ((20, 7, True), 0), ((12, 7, False), 1), ((17, 7, True), 0)]Q,pi,monitored_state_action_values = mc_control(
env,
n_episodes=10,
monitored_state_actions=monitored_state_actions,
diag=True)
episode 1: [((16, 10, False), 1, -1)]
-episode_state_actions: [((16, 10, False), 1)]
---t=0 St, At, Rt+1: ((16, 10, False), 1, -1)
G: -1.0
((16, 10, False), 1) not in [], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0
episode 2: [((17, 10, False), 1, 0), ((20, 10, False), 1, -1)]
-episode_state_actions: [((17, 10, False), 1), ((20, 10, False), 1)]
---t=1 St, At, Rt+1: ((20, 10, False), 1, -1)
G: -1.0
((20, 10, False), 1) not in [((17, 10, False), 1)], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0
---t=0 St, At, Rt+1: ((17, 10, False), 1, 0)
G: -1.0
((17, 10, False), 1) not in [], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0
episode 3: [((17, 9, False), 0, 0)]
-episode_state_actions: [((17, 9, False), 0)]
---t=0 St, At, Rt+1: ((17, 9, False), 0, 0)
G: 0.0
((17, 9, False), 0) not in [], processing ...
G_sum[(St,At)]: 0.0
G_cnt[(St,At)]: 1.0
Q[St][At]: 0.0
episode 4: [((20, 4, True), 1, 0), ((20, 4, False), 0, 1)]
-episode_state_actions: [((20, 4, True), 1), ((20, 4, False), 0)]
---t=1 St, At, Rt+1: ((20, 4, False), 0, 1)
G: 1.0
((20, 4, False), 0) not in [((20, 4, True), 1)], processing ...
G_sum[(St,At)]: 1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: 1.0
---t=0 St, At, Rt+1: ((20, 4, True), 1, 0)
G: 1.0
((20, 4, True), 1) not in [], processing ...
G_sum[(St,At)]: 1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: 1.0
episode 5: [((12, 10, False), 1, 0), ((18, 10, False), 0, -1)]
-episode_state_actions: [((12, 10, False), 1), ((18, 10, False), 0)]
---t=1 St, At, Rt+1: ((18, 10, False), 0, -1)
G: -1.0
((18, 10, False), 0) not in [((12, 10, False), 1)], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0
---t=0 St, At, Rt+1: ((12, 10, False), 1, 0)
G: -1.0
((12, 10, False), 1) not in [], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0
episode 6: [((13, 10, False), 1, -1)]
-episode_state_actions: [((13, 10, False), 1)]
---t=0 St, At, Rt+1: ((13, 10, False), 1, -1)
G: -1.0
((13, 10, False), 1) not in [], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0
episode 7: [((13, 1, False), 0, -1)]
-episode_state_actions: [((13, 1, False), 0)]
---t=0 St, At, Rt+1: ((13, 1, False), 0, -1)
G: -1.0
((13, 1, False), 0) not in [], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0
episode 8: [((14, 1, False), 1, -1)]
-episode_state_actions: [((14, 1, False), 1)]
---t=0 St, At, Rt+1: ((14, 1, False), 1, -1)
G: -1.0
((14, 1, False), 1) not in [], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0
episode 9: [((19, 10, False), 1, -1)]
-episode_state_actions: [((19, 10, False), 1)]
---t=0 St, At, Rt+1: ((19, 10, False), 1, -1)
G: -1.0
((19, 10, False), 1) not in [], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0
episode 10: [((16, 7, False), 0, -1)]
-episode_state_actions: [((16, 7, False), 0)]
---t=0 St, At, Rt+1: ((16, 7, False), 0, -1)
G: -1.0
((16, 7, False), 0) not in [], processing ...
G_sum[(St,At)]: -1.0
G_cnt[(St,At)]: 1.0
Q[St][At]: -1.0
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
("G_sum: defaultdict(<class 'float'>, {((16, 10, False), 1): -1.0, ((20, 10, "
'False), 1): -1.0, ((17, 10, False), 1): -1.0, ((17, 9, False), 0): 0.0, '
'((20, 4, False), 0): 1.0, ((20, 4, True), 1): 1.0, ((18, 10, False), 0): '
'-1.0, ((12, 10, False), 1): -1.0, ((13, 10, False), 1): -1.0, ((13, 1, '
'False), 0): -1.0, ((14, 1, False), 1): -1.0, ((19, 10, False), 1): -1.0, '
'((16, 7, False), 0): -1.0})')
("G_cnt: defaultdict(<class 'float'>, {((16, 10, False), 1): 1.0, ((20, 10, "
'False), 1): 1.0, ((17, 10, False), 1): 1.0, ((17, 9, False), 0): 1.0, ((20, '
'4, False), 0): 1.0, ((20, 4, True), 1): 1.0, ((18, 10, False), 0): 1.0, '
'((12, 10, False), 1): 1.0, ((13, 10, False), 1): 1.0, ((13, 1, False), 0): '
'1.0, ((14, 1, False), 1): 1.0, ((19, 10, False), 1): 1.0, ((16, 7, False), '
'0): 1.0})')
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
monitored_state_action_values: defaultdict(<class 'list'>, {((21, 7, False), 0): [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], ((20, 7, True), 0): [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], ((12, 7, False), 1): [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0], ((17, 7, True), 0): [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]})Qdefaultdict(<function __main__.mc_control.<locals>.<lambda>>,
{(12, 7, False): array([0., 0.]),
(12, 10, False): array([ 0., -1.]),
(13, 1, False): array([-1., 0.]),
(13, 10, False): array([ 0., -1.]),
(14, 1, False): array([ 0., -1.]),
(16, 7, False): array([-1., 0.]),
(16, 10, False): array([ 0., -1.]),
(17, 7, True): array([0., 0.]),
(17, 9, False): array([0., 0.]),
(17, 10, False): array([ 0., -1.]),
(18, 10, False): array([-1., 0.]),
(19, 10, False): array([ 0., -1.]),
(20, 4, False): array([1., 0.]),
(20, 4, True): array([0., 1.]),
(20, 7, True): array([0., 0.]),
(20, 10, False): array([ 0., -1.]),
(21, 7, False): array([0., 0.])})pidefaultdict(int,
{(12, 1, False): 1,
(12, 1, True): 1,
(12, 2, False): 1,
(12, 2, True): 1,
(12, 3, False): 1,
(12, 3, True): 0,
(12, 4, False): 1,
(12, 4, True): 0,
(12, 5, False): 1,
(12, 5, True): 0,
(12, 6, False): 0,
(12, 6, True): 1,
(12, 7, False): 0,
(12, 7, True): 1,
(12, 8, False): 0,
(12, 8, True): 0,
(12, 9, False): 1,
(12, 9, True): 1,
(12, 10, False): 0,
(12, 10, True): 1,
(13, 1, False): 1,
(13, 1, True): 0,
(13, 2, False): 1,
(13, 2, True): 1,
(13, 3, False): 1,
(13, 3, True): 1,
(13, 4, False): 0,
(13, 4, True): 0,
(13, 5, False): 1,
(13, 5, True): 0,
(13, 6, False): 1,
(13, 6, True): 1,
(13, 7, False): 0,
(13, 7, True): 1,
(13, 8, False): 1,
(13, 8, True): 1,
(13, 9, False): 1,
(13, 9, True): 1,
(13, 10, False): 0,
(13, 10, True): 1,
(14, 1, False): 0,
(14, 1, True): 0,
(14, 2, False): 0,
(14, 2, True): 0,
(14, 3, False): 0,
(14, 3, True): 1,
(14, 4, False): 0,
(14, 4, True): 0,
(14, 5, False): 0,
(14, 5, True): 0,
(14, 6, False): 0,
(14, 6, True): 1,
(14, 7, False): 0,
(14, 7, True): 0,
(14, 8, False): 1,
(14, 8, True): 1,
(14, 9, False): 1,
(14, 9, True): 1,
(14, 10, False): 0,
(14, 10, True): 1,
(15, 1, False): 1,
(15, 1, True): 1,
(15, 2, False): 1,
(15, 2, True): 0,
(15, 3, False): 1,
(15, 3, True): 0,
(15, 4, False): 0,
(15, 4, True): 0,
(15, 5, False): 0,
(15, 5, True): 0,
(15, 6, False): 1,
(15, 6, True): 1,
(15, 7, False): 1,
(15, 7, True): 1,
(15, 8, False): 1,
(15, 8, True): 0,
(15, 9, False): 1,
(15, 9, True): 0,
(15, 10, False): 0,
(15, 10, True): 0,
(16, 1, False): 1,
(16, 1, True): 0,
(16, 2, False): 1,
(16, 2, True): 0,
(16, 3, False): 1,
(16, 3, True): 0,
(16, 4, False): 0,
(16, 4, True): 0,
(16, 5, False): 0,
(16, 5, True): 1,
(16, 6, False): 0,
(16, 6, True): 0,
(16, 7, False): 1,
(16, 7, True): 1,
(16, 8, False): 1,
(16, 8, True): 1,
(16, 9, False): 0,
(16, 9, True): 1,
(16, 10, False): 0,
(16, 10, True): 1,
(17, 1, False): 1,
(17, 1, True): 0,
(17, 2, False): 0,
(17, 2, True): 1,
(17, 3, False): 1,
(17, 3, True): 0,
(17, 4, False): 1,
(17, 4, True): 0,
(17, 5, False): 0,
(17, 5, True): 1,
(17, 6, False): 0,
(17, 6, True): 1,
(17, 7, False): 0,
(17, 7, True): 0,
(17, 8, False): 1,
(17, 8, True): 1,
(17, 9, False): 0,
(17, 9, True): 0,
(17, 10, False): 0,
(17, 10, True): 1,
(18, 1, False): 1,
(18, 1, True): 1,
(18, 2, False): 1,
(18, 2, True): 0,
(18, 3, False): 0,
(18, 3, True): 0,
(18, 4, False): 1,
(18, 4, True): 0,
(18, 5, False): 1,
(18, 5, True): 0,
(18, 6, False): 0,
(18, 6, True): 1,
(18, 7, False): 0,
(18, 7, True): 1,
(18, 8, False): 1,
(18, 8, True): 1,
(18, 9, False): 1,
(18, 9, True): 0,
(18, 10, False): 1,
(18, 10, True): 1,
(19, 1, False): 0,
(19, 1, True): 0,
(19, 2, False): 0,
(19, 2, True): 1,
(19, 3, False): 0,
(19, 3, True): 1,
(19, 4, False): 0,
(19, 4, True): 1,
(19, 5, False): 1,
(19, 5, True): 0,
(19, 6, False): 0,
(19, 6, True): 1,
(19, 7, False): 0,
(19, 7, True): 0,
(19, 8, False): 1,
(19, 8, True): 1,
(19, 9, False): 0,
(19, 9, True): 1,
(19, 10, False): 0,
(19, 10, True): 1,
(20, 1, False): 0,
(20, 1, True): 1,
(20, 2, False): 1,
(20, 2, True): 1,
(20, 3, False): 1,
(20, 3, True): 0,
(20, 4, False): 0,
(20, 4, True): 1,
(20, 5, False): 0,
(20, 5, True): 1,
(20, 6, False): 1,
(20, 6, True): 1,
(20, 7, False): 0,
(20, 7, True): 0,
(20, 8, False): 1,
(20, 8, True): 1,
(20, 9, False): 1,
(20, 9, True): 0,
(20, 10, False): 0,
(20, 10, True): 0,
(21, 1, False): 1,
(21, 1, True): 0,
(21, 2, False): 1,
(21, 2, True): 0,
(21, 3, False): 0,
(21, 3, True): 0,
(21, 4, False): 0,
(21, 4, True): 0,
(21, 5, False): 1,
(21, 5, True): 0,
(21, 6, False): 0,
(21, 6, True): 1,
(21, 7, False): 1,
(21, 7, True): 0,
(21, 8, False): 1,
(21, 8, True): 1,
(21, 9, False): 0,
(21, 9, True): 0,
(21, 10, False): 1,
(21, 10, True): 0})print(monitored_state_actions[0])
print(monitored_state_action_values[monitored_state_actions[0]])((21, 7, False), 0)
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]#
# last value in monitored_state_actions should be value in Q
msa = monitored_state_actions[0]; print('msa:', msa)
s = msa[0]; print('s:', s)
a = msa[1]; print('a:', a)
monitored_state_action_values[msa][-1], Q[s][a] #monitored_stuff[msa] BUT Q[s][a]msa: ((21, 7, False), 0)
s: (21, 7, False)
a: 0(0.0, 0.0)5.5 Run 1
First, we will run the algorithm for 10,000 episodes, using policy1:
Q1,pi1,monitored_state_action_values1 = mc_control(
env,
n_episodes=10_000,
monitored_state_actions=monitored_state_actions,
diag=False)Episode 10000/10000#
# last value in monitored_state_actions should be value in Q
msa = monitored_state_actions[0]; print('msa:', msa)
s = msa[0]; print('s:', s)
a = msa[1]; print('a:', a)
monitored_state_action_values1[msa][-1], Q1[s][a] #monitored_stuff[msa] BUT Q[s][a]msa: ((21, 7, False), 0)
s: (21, 7, False)
a: 0(0.8974358974358975, 0.8974358974358975)The following chart shows how the values of the 4 monitored state-actions converge to their values:
plt.rcParams["figure.figsize"] = (18,10)
for msa in monitored_state_actions:
plt.plot(monitored_state_action_values1[msa])
plt.title('Estimated $q_\pi(s,a)$ for some state-actions', fontsize=18)
plt.xlabel('Episodes', fontsize=16)
plt.ylabel('Estimated $q_\pi(s,a)$', fontsize=16)
plt.legend(monitored_state_actions, fontsize=16)
plt.show()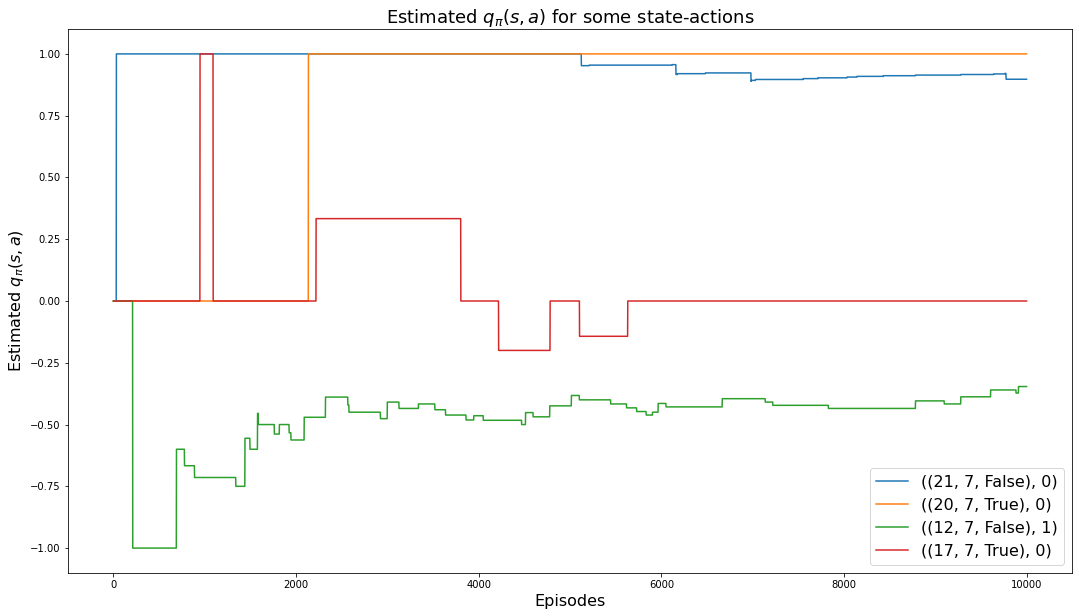
The following charts shows the estimate of the associated estimated optimal state-value function, \(v_*(s)\), for the cases of a usable ace as well as not a usable ace. First, we compute V1 which is the estimate for \(v_*(s)\):
V1 = defaultdict(float)
for state, actions in Q1.items():
action_value = np.max(actions)
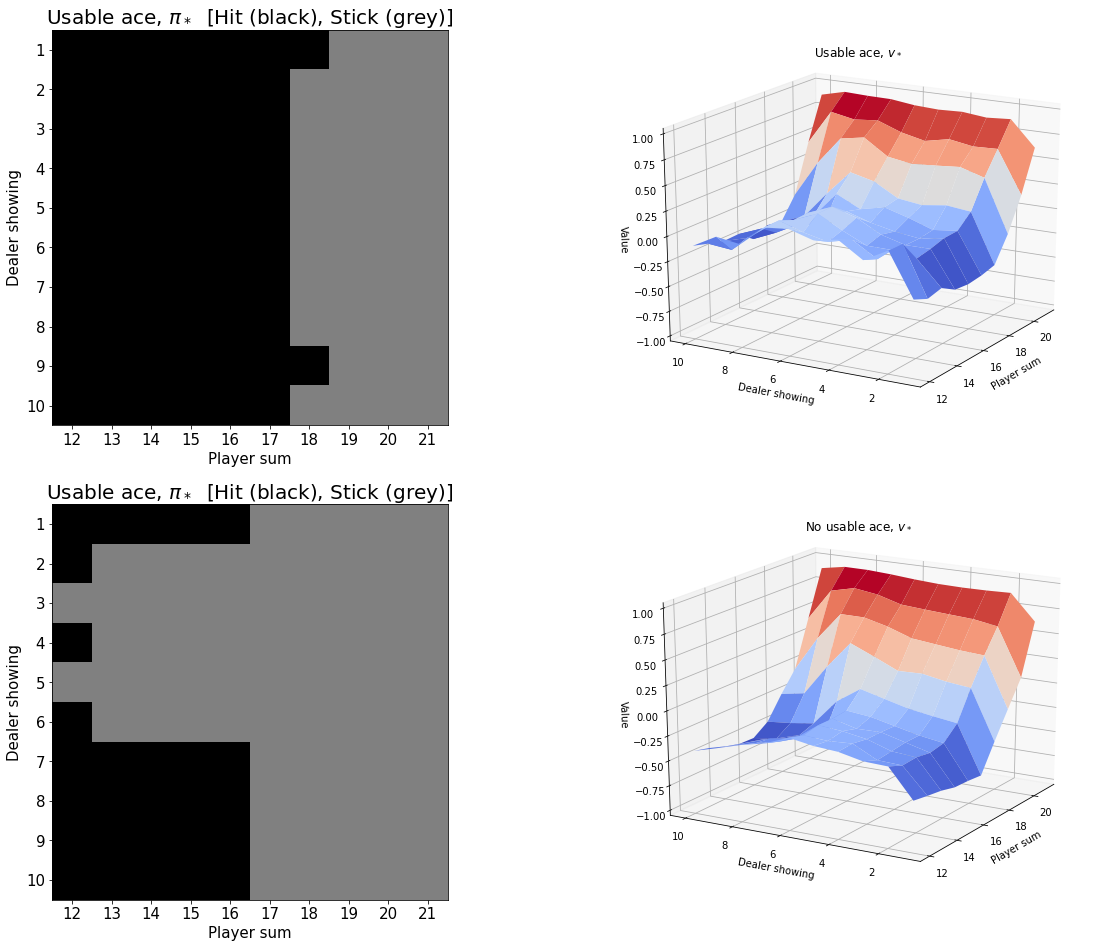
V1[state] = action_valueAZIM = -110
ELEV = 20myplot.plot_pi_star_and_v_star(pi1, V1, title="$\pi_* and v_*$", wireframe=False, azim=AZIM-40, elev=ELEV);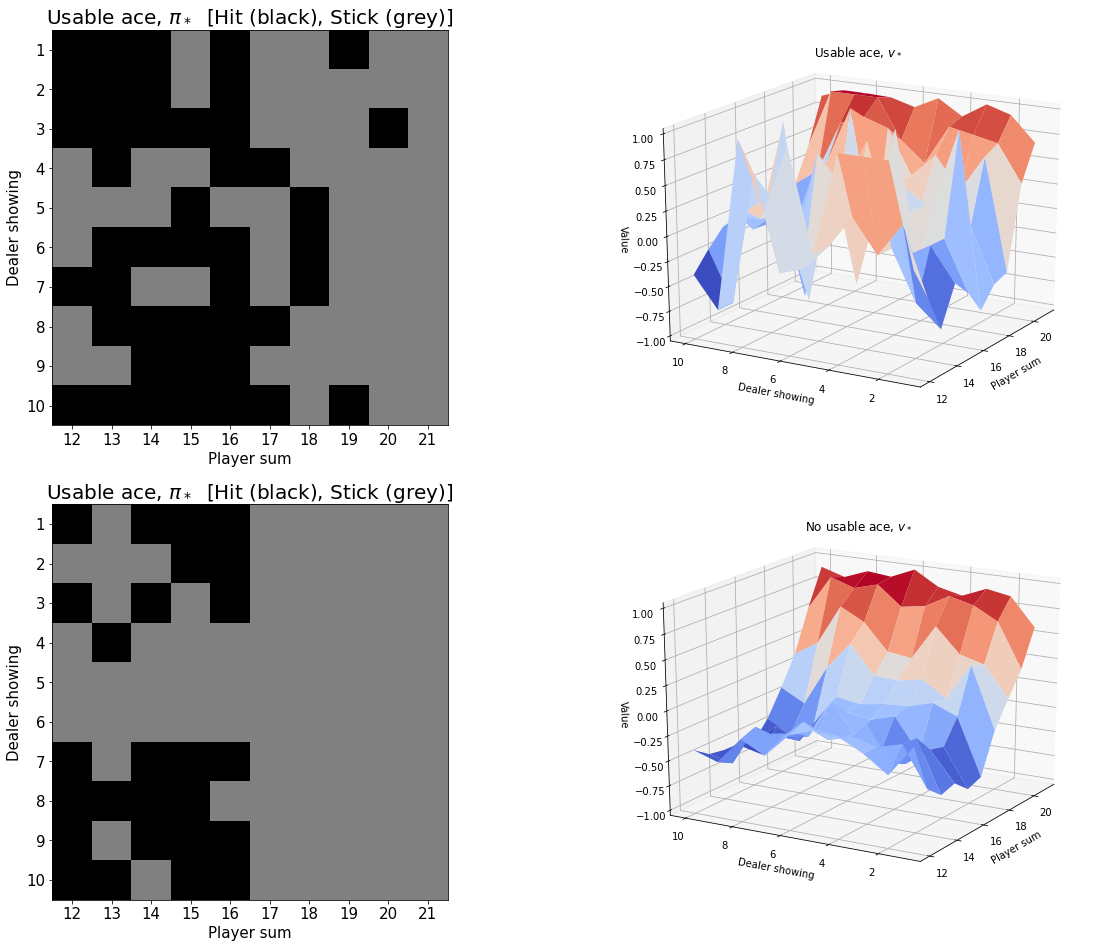
5.6 Run 2
Our final run uses 500,000 episodes and the accuracy of the action-value function is higher.
Q2,pi2,monitored_state_action_values2 = mc_control(
env,
n_episodes=500_000,
monitored_state_actions=monitored_state_actions,
diag=False)Episode 500000/500000#
# last value in monitored_state_actions should be value in Q
msa = monitored_state_actions[0]; print('msa:', msa)
s = msa[0]; print('s:', s)
a = msa[1]; print('a:', a)
monitored_state_action_values2[msa][-1], Q2[s][a] #monitored_stuff[msa] BUT Q[s][a]msa: ((21, 7, False), 0)
s: (21, 7, False)
a: 0(0.9214387127307146, 0.9214387127307146)plt.rcParams["figure.figsize"] = (18,12)
for msa in monitored_state_actions:
plt.plot(monitored_state_action_values2[msa])
plt.title('Estimated $q_\pi(s,a)$ for some state-actions', fontsize=18)
plt.xlabel('Episodes', fontsize=16)
plt.ylabel('Estimated $q_\pi(s,a)$', fontsize=16)
plt.legend(monitored_state_actions, fontsize=16)
plt.show()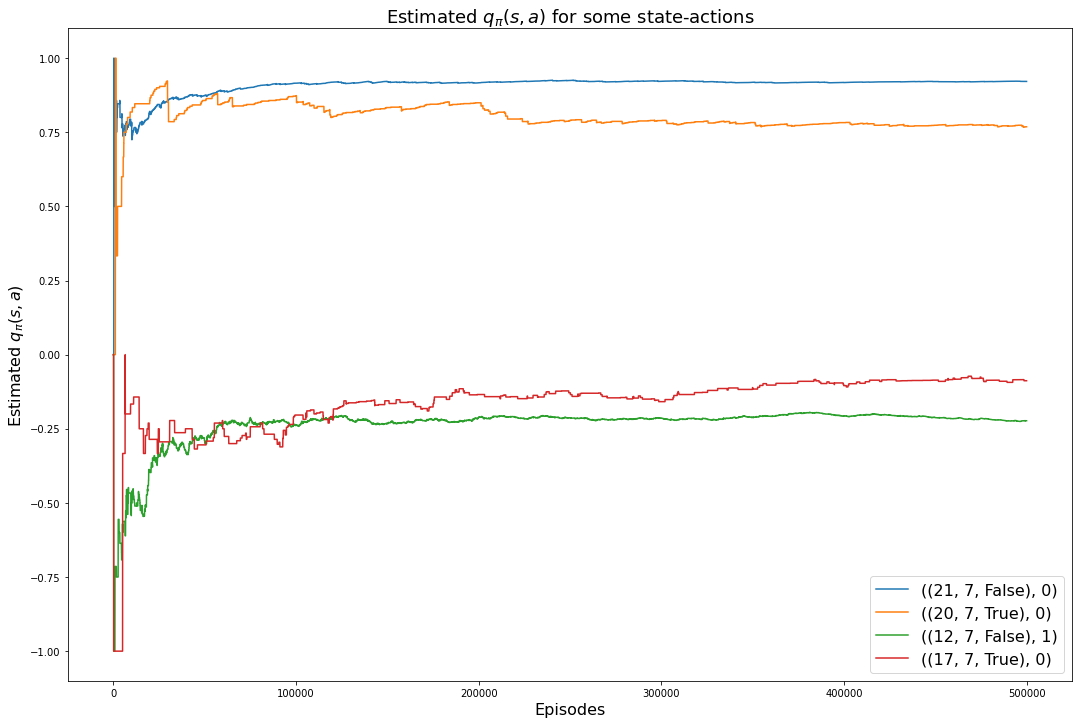
V2 = defaultdict(float)
for state, actions in Q2.items():
action_value = np.max(actions)
V2[state] = action_valuemyplot.plot_pi_star_and_v_star(pi2, V2, title="$\pi_* and v_*$", wireframe=False, azim=AZIM-40, elev=ELEV);